This paper seeks to demonstrate that single units/multiunits and local field potentials in M1 are modulated by reward expectaiton during reaching movements and that this modulation is present even while subjects passively viewed cursor motions that are predictive of either reward or nonreward. They also tried to classify whether a trial is rewarding vs. nonrewarding based on the neural data, on a moment-to-moment basis.
Experiments:
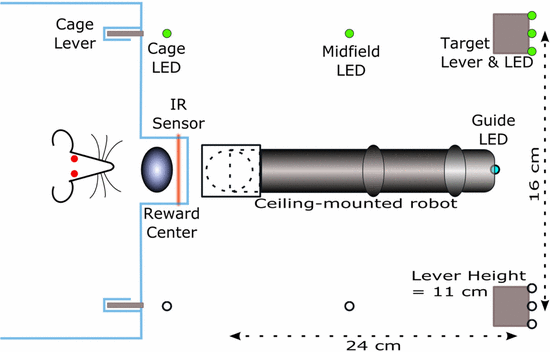
Monkey arm wears an exoskeletal robot through all tasks. Use a single target during all trials
-
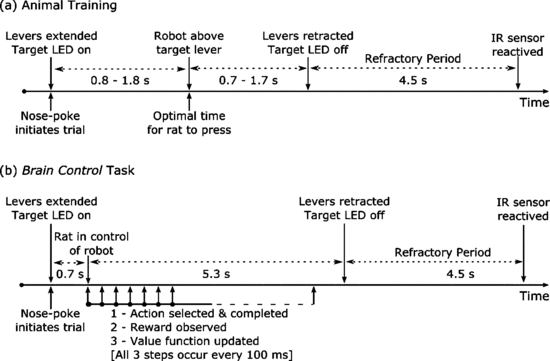
Manual Task. The monkey was required to hold at the center target for 325ms before teh peripheral target appeared, then hold an additional 300ms before the center target disappearted, the go cue appearing for moving to the peripheral target, and hold for 325ms before receiving a liquid reward or no reward.
The paper does not manually control for monkey arm trajectory, speed, etc. But in offline analysis they selected kinematically indistinguishable trajectories between the two reward contingencies to isolate the effect of reward.
-
OT1. Monkey arm is fixed by the robot and cannot move. The monkey would fixate at the center target and observe the center target change color; red represents a rewarding trial, blue represents a nonrewarding trial. The cursor would then move toward the peripheral target at a constant speed with movement toward a red target resulitng in a reward, once the cursor arrived inside the target. For blue targets, reward was withheld. The monkey had to view the target plane to start a trial and maintain visual gaze until the color cue was given.
-
OT2. The monkey observed the cursor moving away or twoard a target with movement toward a the target resulting in a reward, once the cursor arrived inside the target. No reward otherwise.
Results:
Some neurons fired higher throughout reward trials, while others behaved the opposite way. Both contralateral and ipsilateral M1 contains units that simultaneously correlat with reward and kinematics during reaching and observation...but how to identify which is reward-modulated in a less controlled BMI experiment?
Classifiers were trained using PCA components to classify reward vs. nonreward trials. The average classifer performance (over trial length) is around 70%, pretty good.
Simulated RL-BMI using TD-learning, NN for action-reward mappings. Works well, not too surprising, but not too much value either with a two-state classification task.
References to Read
- Dura-Bernal S, Chadderdon GL, Neymotin XZ, Przekwas A, Francis JT, Lytton WW (2014) IEEE Signal Processing in Medicine and Biology Symposium (SPMB'13) Virtual musculoskeletal arm and robotic arm driven by a biomimetic model of sensorimotor cortex with reinforcement learning
- Hosp JA, Pekanovic A, Rioult-Pedotti MS, Luft AR (2011) Dopaminergic projections from midbrain to primary motor cortex mediate motor skill learning. J Neurosci 31:2481–2487.
- Legenstein R, Chase SM, Schwartz AB, Maass W (2010) A reward-modulated hebbian learning rule can explain experimentally observed network reorganization in a brain control task. J Neurosci 30:8400–8410.
- Todorov E, Jordan MI (2002) Optimal feedback control as a theory of motor coordination. Nat Neurosci 5:1226–1235.