Feb 26, 2023 - PCA vs. FA: Theoretical and practical differences

I remember spending an afternoon understanding the theoretical and pratical differences between PCA and FA several years ago, when factor analysis (FA) started to appear more frequently in neuroscience and BMI literature. It was confusing because it seemingly measured the same thing as the popular tool principal component analysis (PCA), but in a much more computationally complex way. When I tried FA on the neural data I was working on at the moment, I didn't see much difference -- reconstruction using the top-n PC components and the assumed n common factors accounted for similar amount of variance in the data.

Reading the recent paper relating neuronal pairwise correlations and dimensionality reduction made me double back on this again -- the motivation question was can we derive similar results using PCA? The answer was no, and looking into this deepened my understanding of these two tools.

Problem Formulation

Both PCA and FA seek to provide a low-rank approximation of a given covariance (or correlation) matrix. "Low-rank" means that only a limited number of principal components or latent factors is used. If we have a $n\times n$ covariance matrix of the data $\mathbf{C}$, then we have the following model formulations:

Here $\mathbf{W}$ is a matrix with $k$ columns ( $k<n$), representing the low number of principal components or latent factors, $\mathbf{I}$ is identify matrix, and $\mathbf{\Psi }$ is a diagnal matrix. Each method can be formulated as finding $\mathbf{WW}$ (in FA's case, als $\mathbf{\Psi }$) to minimize the norm of the difference between left-hand and right-hand sides.

Note that PPCA can be thought of as an intermediate between PCA and FA, where the noise term ${\sigma }^2\mathbf{I}$ makes it a generative model like FA, it practically acts like PCA (in that $\mathbf{W}$ spans the same subspace in both).

Difference in model assumptions

The principal components of PCA are derived from a linear combination of the feature vectors, akin to rotation (and scaling) of the feature-space. The directions of the PC are those where variance is maximized. The interpretation of the PCs, however, may correspond to some subjectively meaningful constructs, but this is not guaranteed in the model assumption.

In contrast, FA is a generative model with the built-in assumption that a number of latent factors led to the observed features. The factors are usually derived from EM algorithms assuming the distribution of the data is generated according to multi-variate Gaussians.

Consequences

FA reconstructs and explains all the pairwise covariances with a few factors, while PCA cannot do it successfully. This is because PCA extracts eigenvectors of the data distribution, while FA seeks to find latent factors that maximizes the covariances explained. Note that it doesn't make much sense to treat the factors from FA as a "direction" in the feature space as in PCA because it's not a transformation of the feature space.

A very useful illustration is given in ttnphns' stackexchange post, showing this difference:

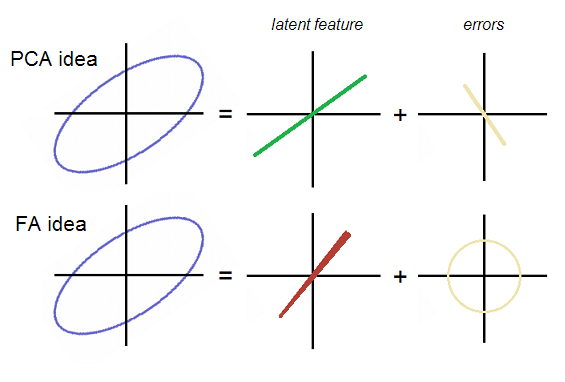
The error of reconstruction using either PC1 or F1 will have different shape in the feature space. The error resulting from FA reconstruction are uncorrelated in the feature space, while that from PCA reconstruction is.

Applications

When to use PCA vs. FA?

Ideally, if the goal is find latent explainatory variables, then FA's generative model assumption is better suited. If the goal is to perform dimensionality reduction, such as when trying to conduct regression model with highly correlated features, PCA would be preferred.

So why would so many papers use PCA instead of FA, and interpret principal components to represent some latent factors?

The interpretation here is theoretically not sound. But practically this is ok, since as the number of features $n$ increases, the results of PCA approaches FA. See amoeba's great simulations on stackexchange, as well as ttnphns's simulations.

Why is this the case, if the model formulation and computations are so different? Referencing amoeba --

From model formulations, PCA finds $\mathbf{W}$ to best approximate the sample covariance matrix such that $\mathbf{C}\approx \mathbf{W}{\mathbf{W}}^T$, while FA finds $\mathbf{W}$ to best approximate the off-diagonal entries of $\mathbf{C}$, i.e. $offdiag(\mathbf{C})\approx \mathbf{W}{\mathbf{W}}^T$ (remember that FA tries to capture the pairwise correlation between features). The diagonal elements of $\mathbf{C}$ in FA is taken care of by $\mathbf{\Psi }$.

This means:

1. If the diagonals of $\mathbf{C}$ are small (i.e. all features have low noise), meaning that the off-diagonal elements dominate $\mathbf{C}$, then FA approaches PCA.
2. If $n$ is very big, then the size of $\mathbf{C}$ is also very big, and therefore the contribution of the diagonal elements is small compared to that of the off-diagonal elements, then once again PCA results approach FA. A good way to think about this is in terms of the residual reconstruction error picture -- when $n\to \mathrm{\infty }$, the residual error from PC-reconstruction becomes more isotropic, approaching that of FA.

When is $n$ large enough for PCA to approximate FA?

When the ratio $n/k$, where $k$ is the expected number of latent factors, is big. Usually a ratio of 10 is a good threshold from simulation results. This also explains my past observations in neural data -- where the number of features is ~100 (number of neurons), and latent factors is ~10 (cursor/actuator position/velocity).

The other, more practical reason is simply that PCA is way more easier to compute!

If PCA approaches FA under large n, why use FA at all?

Beyond better model assumptions for the question investigation, FA formulations enables easier interpretation of shared covariances and its relationship with pairwise correlations. This was the key insight in Umakantha2021, for example.

Conclusions

1. PCA and FA differ in model assumptions, notably, FA assumes the data is generated by some underyling latent factors.
2. PCA seems to approximate the data distribution while minimizing the diagonal reconstruction errors of the covariance matrix, while FA seeks to minimize the offdiagonal reconstruction errors of the covariance matrix.
3. PCA approaches FA results when the number of features is big compared to the assumed number of latent factors.