Classifier performance in primary somatosensory cortex towards implementation of a reinforcement learning based brain machine interface, submitted to Southern Biomedical Engineering Conference, 2016.

In the theme of RL-based BMI decoder, this paper evaluates classifiers for identifying the reinforcing signal (or ERS according to Millan). Evaluates the ability of several common classifiers to detect impending reward delivery within S1 cortex during a grip force match to sample task performed by monkeys.

Methods

1. Monkey trained to grip right hand to hold and match a visually displayed target.

2. PETHs from S1 generated, from 1) aligning with timing of visual cue denoting the impending result of trial (reward delivered or withheld), 2) aligning with timing of trial outcome (reward delievery or withold).

   PETH time extended 500ms after stimulus of interest using a 100ms bin width. (So only 500ms total signal, 5-bin vector samples).

3. Dimension-reduction of PETH via PCA. Use only the first 2 PCs, feed into classifiers including:

   • Naive Bayes
   • Nearest Neighbor (didn't specify how many k...or just one neighbor..)
   • Linear SVM
   • Adaboost
   • Quadratic Discriminant Analysis (QDA)
   • LDA

   Trained on 82 trials, tested on 55 trials. Goal is to determine if a trial is rewarding or non-rewarding.

Results

1. For all classifiers, post-cue accuracy higher than post-reward accuracy. Consistent with previous work (Marsh 2015) showing the presence of conditioned stimuli in reward prediction tasks shift rerward modulated activity in the brain to the earliest stimulus predictive of impending reward delivery.

2. NN performs the best out of all classifiers. But based on the sample size (55 trials) and the performance figures, not significantly better.

Takeaways

Results are good, but should have more controlled experiments to eliminate confounds...could be seeing an effect of attention level.

Also, still limited to discrete actions.

Neural correlates of decision variables in parietal cortex

Motivation

Sensory-motor reflex has been tacitly accepted by many older physiologists as an appropriate model for describing the neural processes that underlie complex behavior. More recent findings (in the 1990s) indicate that, at least in some cases, the neural events that connect sensation and movement may involve processes other than classical relfexive mechanisms and these data suppport theoretical approaches that have challenged reflex models directly.

Researchers outside physiology have long argued (since 1960s) for richer models of the sensory-motor process. These models invok3 the explicit representation of a class of decision variables, which carry information about the environment, are extracted in advance of response selection, aid in the interpretatin or processing of sensory data and are a prerquisite for rational decision making.

This paper describes a formal economic-mathematical approach for the physiological studey o fthe senosry-motor process/decision-making, in the lateral intra-parietal (LIP) area of the macaque brain.

Caveats

1. Expectation of reward magnitude result in neural modulations in the LIP. LIP is known to translate visual signals into eye-movement commands.

2. The same neurons are sensitive to expected gain and outcome probability of an action. Also correlates with subjective estimate of the gain associated with different actions.

3. These indicate neural basis of reward expectation.

Decision-Making Framework

The rational decision maker makes decision based on two environmental variables: the gain expected to result from an action, and the probability that the expected gain will be realized. The decision maker aims to maximize the expected reward.

Neurobiological models of the processes that connect sensation and action almost never propose the explicit representation of decision variables by the nervous system. Authors propose a framework containing

1. Current sensory data - reflect the observer's best estimate of the current state of the salient elements of the environment.

2. Stored representation of environmental contingencies - represent the chooser's assumptions about current environmental contingencies, detailing how an action affects the chooser.

This is a Bayesian framework.

Sensory-Motor integration in LIP

In a previous experiment, the authors concluded that visual attention can be treated as conceptually separable from other elements of the decision-making process, and that activity in LIP does not participate in sensory-attentional processing but is correlated with either outcome continguencies, gain functions, decision outputs or motor planning.

Experiments

1. Cue saccade trials: a change in the color of a centrally located fixation stimulus instructed subjects to make one of two possible eye-movement responses in order to receive a juice reward. Before the color change, the rewarded movement was ambiguous. The successive trials, the volume of juice delivered for each instructed response (expected gain), or the probability that each possible response would be instructed (outcome probability) are varied.

   Goal is to test whether any LIP spike rates correlate to variations in these decision variables.

2. Animals were rewarded for choosing either of two possible eye-movement responses. In subsequent trials, varied the gain that could be expected from each possible response. The frequency with which the animal chose each response is then an estimate of the subjective value of each option.

   Goal is to test whether any LIP activity variation correlates with the subjective estimate of decision variable.

Analysis

Experiment 1

For each condition: 1) keeping outcome probability fixed while varying expected gain, and 2) keeping expected gain fixed while varying outcome probability, a trial is divded into 6 200ms epochs. The activity during these epochs are then used to calculate regressions of the following variables:

1. Outcome probability.
2. Expected gain.
3. Type of movement made (up or down saccade).
4. Amplitude of saccade.
5. Average velocity of saccade.
6. Latency of saccade.

Multiple regression were done for each epoch, percentage of recorded neurons that show significant correlations between firing rate and the decision variables were calculated.

Average slope of regression against either decision variables were taken as a measure of correlation. The same regressio slopes were calculated for type of movement made as well.

For both expected gain and outcome probability, the regression slopes were significantly greater than 0, and greater than that for type of movement during early and late visual intervals, and decay during late-cue and movement. The opposite is seen for type of movement regression slopes.

Experiment 2

Similar analysis is done to evaluate neural correlate of subjective estimate of reward. Results show activity level correlates with the perceived gain associated with the target location within the neuron's receptive field. The time evolution of the regression slopes show a similar decay as before.

Consistent with Herrnstein's matching law for choice behavior, there was a linear relationship between the proportion of trials on which the animal chose the target inside the response field and the proportion of total juice available for gaze shifts to that target.

Animal's estimate of the relative value of the two choices is correlated with the activation of intraparietal neurons.

Discussions

1. It would seem obvious that there are neural correlates for decision variables, rather than the traditional sensory-motor reflex decision-making framework. But this may be solely in the context of investigating sensory areas..probably have to read Sherrington to know how he reached that conclusion.

2. The data in this paper can be hard to reconcile with traditional sensory-attentional models, which would attribute modulations in the activity of visually responsive neurons to changes in the behavior relevance of visual stimuli, which would then argue that the author's manipulations of expected gain and outcome probably merely altered the visual activity of intraparietal neurons. Explainations include:

   • Previous work show intraparietal neurons are insensitive to changes in the behavioral relevance of either presented stimulus when it is not the target of a saccade.

   • Experiment 2 showed that intraparietal neuron activity was modulated by changes in the estimated value of each response during the fixation intervals BEFORE the onset of response targets.

3. Modulations by decision variables early in trial. Late in trial more strongly modulated by movement plan. Suggests intraparietal cortex lies close to the motor output stages of the sensory-deicsion-motor process. Prefrontal cortex perhaps has reprsentation of decision variables throughout the trial.

Parietal Lobe: From Action Organization to Intention Understanding

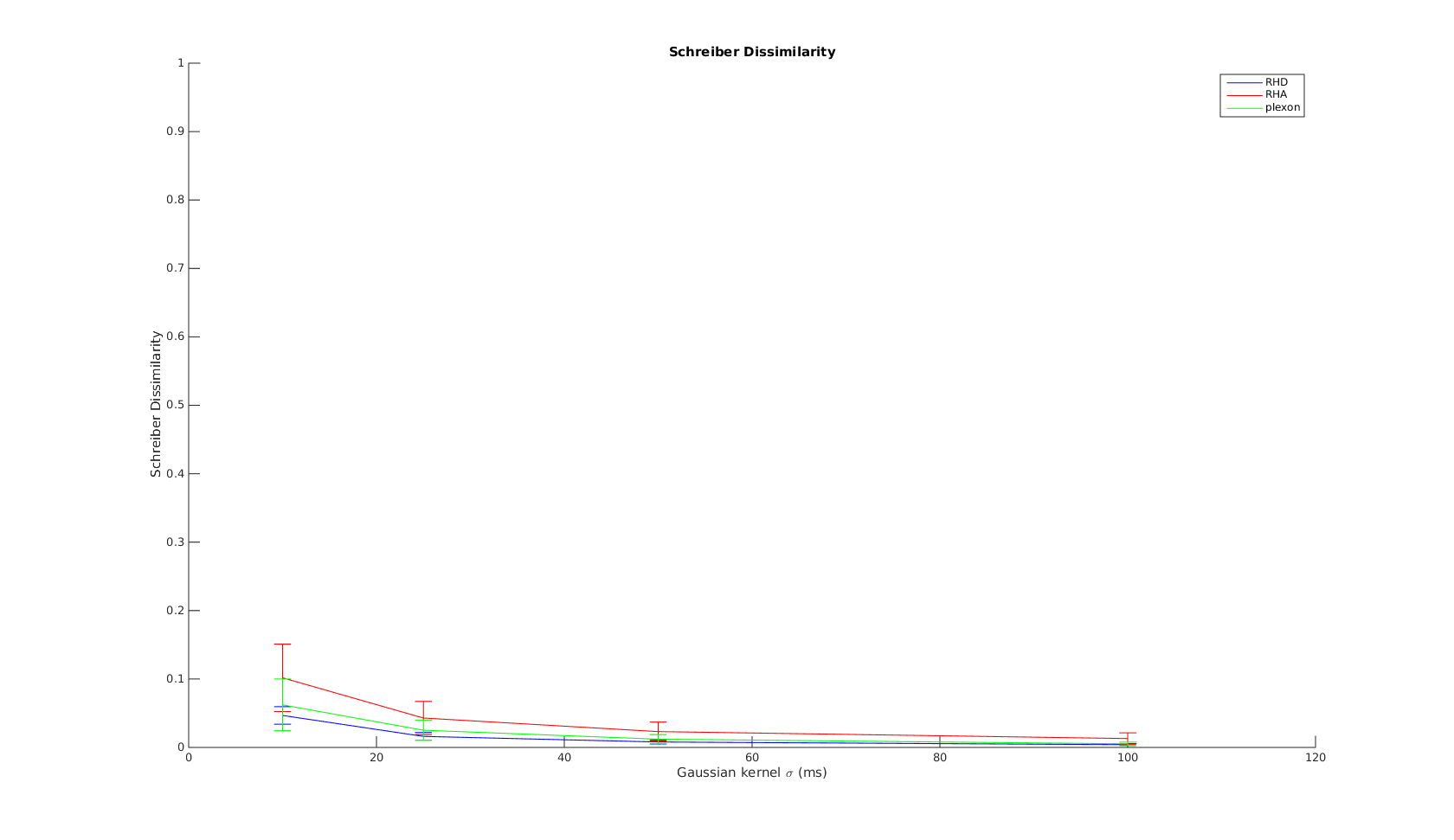
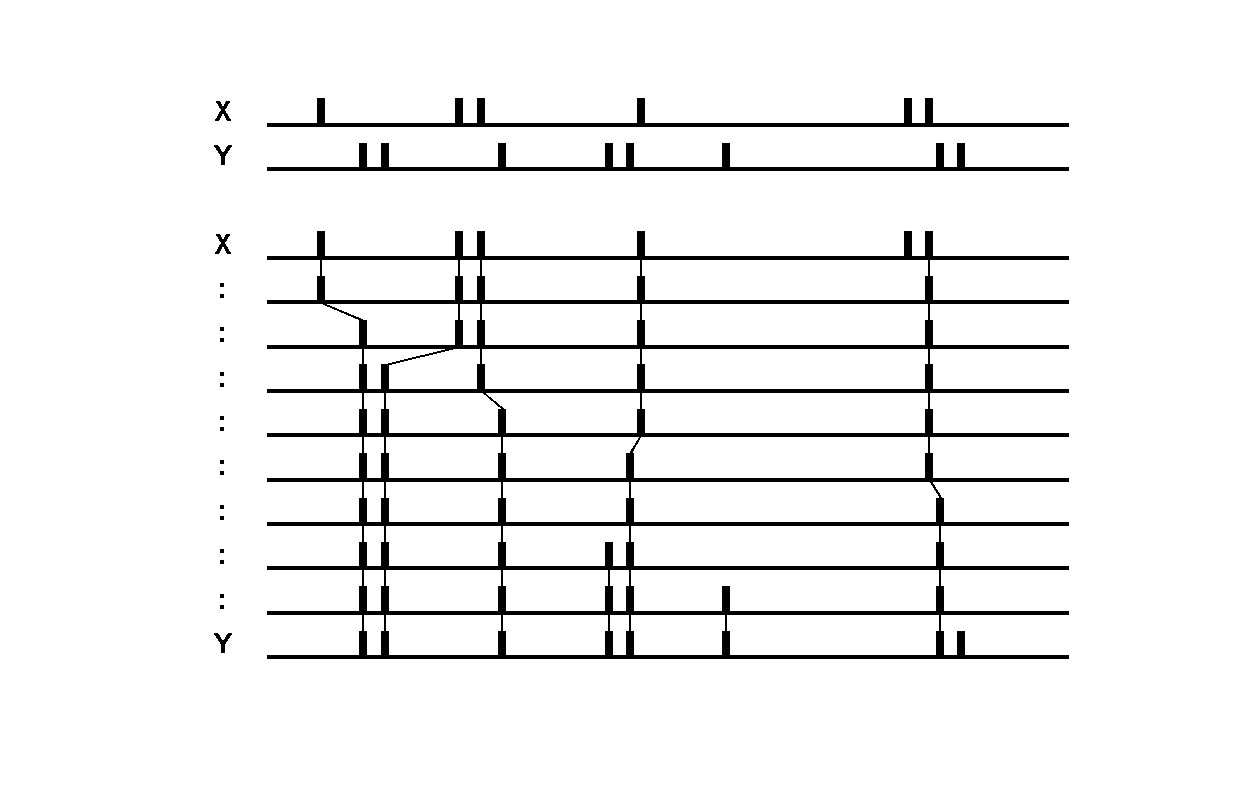
Inferior parietal lobule (IPL) neurons were studied when monkeys performed motor acts embedded in different actions, and when they observed similar acts done by an experimenter. Most IPL neurons coding a specific act (e.g. grasping) showed markedly different activiations depending on contexts (e.g. grasping for eating or for placing).

Many motor IPL neurons also discharged during the observation of acts done by others. The context-dependence also applied to when these actions were observed.

These neurons fired during the observation of an act, before the beginning of the subsequent acts specifying the action - thus these neurons not only code the observed motor acts but also allow the observer to understand the agent's intentions.

Posterial parietal cortex has traditionally been considered as the association cortex. Besides "putting together" different sensory modalities, also

1. Codes motor actions
2. Provides the representations of these motor actions with specific sensory information.

Experiment

Set 1

Investigates neuron selectivity during actioin performance:

1. Monkey starts from a fixed position, reache for and grasp a piece of food located in front of it and brigh the food to mouth.
2. Monkey reach for and grasp an object, and place it in a box on the table.
3. Monkey reach for and grasp an object, and place it into a container near its mouth.

Most observed neurons discharged differentially with respect to context.

Control for confounds:

1. Grasp an identical piece of food in both conditions - rewarded with the same piece of food in situation 2.
2. Situation 3 aims to determine if arm kinematics determined the different firing behavior - turns out to be pretty much identical to situation 2.
3. Force exerted grasping - mechanical device that could hold the objects with two different strengths used, no change in neuron selectivity.

Set 2

Study 41 mirror neurons that discharge both during grapsing observation and grasping execution, in an experiment where the monkey observed an experimenter performing those actions.

Results:

1. Some neurons are selective for grasping to eat, others for grasping to place - most have the same specificity as when the monkey performed those actions.
2. Most neurons have the same selectivity regardless of whether the grasped object is food or solid. Some discharged more strongly in the placing conditions when the grasped object was food.

The authors suggest that while counter-intuitive, this should makes sense since motor acts are not related to one another independent of the global aim of the action but appear to form prewired intentional chains in which each motor act is faciliatted by the previously executed one. This reminds me of Churchland and Shenoy's theory about action planning as a trajectory in the Null-Space.

Consequences

The authors suggest that the monkey's decision on what to do with the object is undoubtedly made before the onset of the grasping movement. The action intentionis set before the beinning of the movements and is already reflected in the first motor act. This motor reflectioin of action intention and the chained motor organization of IPL neurons have profound consequences on [...] understanding the intention of others.

While I can see where he reaches this conclusion, and it would nicely explain why passive observation training for BMI works (even though mostly M1 and S1 neurons are recorded), but this explanation would make more sense if most of the difference in discharge rate happens BEFORE the monkey physically grasp the object/food...

It has been generally accepted that mirror neurons allow the observing individual to understand the goal of the observed motor act. The authors' interpretation then deduces that because the monkey knows the outcome of the motor act it executes, it recognizes the goal of the motor act done by another individual when this act triggers the same set of neurons that are active during the execution of that act.

Applications to BMI

This paper suggests mirror neurons as a mechanism for evaluation of intention, it also suggests that depending on context and object, a simple grasp action may be coded differently. Thus a BMI arm trained on passive observation of grasping an object to place might not work well when the user tries to grasp a food to eat. This is similar to when the Schwarz 10-DOF arm encountered, when the human subject had trouble grasping object. The problem only went away when the training was done in a virtual space.

Errare machinale est: the use of error-related potentials in braine-machine interfaces

This review focuses on electrophysiological correlates of error recognition in human brain, in the context of human EEG. Millan calls this error-related potentials, ErrPs. It has been proposed to use these signals to improve BMI, in the form of training BMI decoder via reinforcement learning.

Error-related brain activity

Early reports in EEG date back to early 1990's (Falkenstein et al., 1991; Gehring et al., 1993). Showed a characteristic EEG event-related potential elicited after subjects commited errors in a speed repsonse choice task, characterized by a negative potential deflection, termed the error-related negativity, appearing over fronto-central scalp areas at about 50-100ms after a subject's erroneous response. The negative copmonent is followed by a centro-parietal positive deflection.

Modulations of this latter component have been linked to the subject's awareness of the error. ERN amplitude seems to be modulated by the importance of erros in the given task. These signals have been shown to be quite reliable over time and across diferent tasks.

Very encouraging for reinforcement-learning based schemes.

fMRI, EEG-based source localization, and intra-cranial recordings suggest that the fronto-central ERP modulations commonly involve the medial-frontal cortex, specifically the anterior cingulate cortex (ACC). This is consistent with ACC being involved in reward-anticipation and decision-making.

Error-related potentials for BMI

Ferrez and Millan 2008: 2-class motor-imagery bsaed BMI controlling a cursor moving in discrete steps -- showed ERPs elicited after each command could be decoded as corresponding to the error or correct condition with an accuracy of about 80%. Only 5 subjects, but encouraging.

The ErrP classifiers maintained the same performance when tested several months after calibration - relatively stable signal form. Seemed to be mainly related to a general error-monitoring process, not task-dependent.

Possible Confounds (in EEG studies):

1. Eye movement contamination: Need to make sure location or movement of target stimuli are balanced.
2. Observed potentials are more related to the rarrity of the erroneous events (?)
3. Attential level: subjects tend to have smaller ErrP amplitude when simply monitoring the device than when they are controling it -- requires efficient calibration methods.

Error-Driven Learning

Trials in which the decoder performed correctly, as classified by ErrP can be incorporated into a learning set that can be then used to perform online retraining of the motor imagery (MI) classifier. Rather discrete, but good architecture.

Binary ErrP decoding can be affected substantially by false positive rate (i.e. correct BMI actions misclassified as errors). Solution is to use methods relying on probabilistic error signals, taking into account of the reliability of the ErrP decoder.

Millan has used ErrP to improve his shared-control BMI systems.

A learning-based approach to artificial sensory feedback leads to optimal integration

Motivation

Maximally precise movements are achieved by combining estimates of limb or target positiion from multiple sensory modalities, weighting each by its relative reliability. Current BMI relies on visual feedback alone, and would be hard to achieve fluid and precise natural movements. Artificial proprioception may improve performance of neuroprosthetics.

Goal

Artificial proprioception should be able to:

1. Provide sufficient information to alow competent performance in the absence of other sensory inputs.
2. Permit multisensory integration with vision to reduce movement variability when both signnals are available.
   Implemented via multichannel intracortical microstimulation. Different from most other works that take a biomimetic approach. It focuses not on reproducing natural patterns of activity but instead on taking advantage of the natural mechanisms of sensorimotor learning and plasiticity.

Hypothesize spatiotemporal correlations between a visual signal and novel artificial signal in a behavioral context would be sufficient for a monkey to learn to integrate the new modality.

Approach

Monkey looks at a screen, trying to move to an invisible target. The movement vector is the vector between the monkey's current hand position and the invisible target.

1. Visual feedback: The movement vector is translated to random moving-dot flow field. The coherence of the dot-field is the percentage of dots moving in the same direction. So 100% coherence dot-field would have the dots moving in the same direction as the movement vector.
2. ICMS: 96-channels array is implanted. 8 electrodes were stimulated on. During feedback, the movement vector is decomposed into 8 components in direction equally spaced around a circle, each corresponding to a stimulating electrode. Higher relative frequency on an electrode means greater component of the movement vector in that direction. Common frequency scaling factor corresponds to movement vector distance.

Experiments inluded:

1. Learning the task with only visual feedback, with different coherence to demonstrate performance differences due to changing sensory cue precision.
2. Learning the task with only ICMS feedback. Trained by providing ICMS during visual task to teach monkey to associate the spatial relationship. No changing coherence.
3. Performing the task with both.

Metrics:

1. Percent trials correct
2. Number of movement segments - small is better. Movement segment found by assuming sub-movements have bell-hsaped velocity profiles -- identify submovements by threshold crossings of the radio velocity plot of a trajectory.
3. Normalized movement time: by the distance to target.
4. Noramlized path length: Normalized the integrated path length by the distance from start to target.
5. Mean and Variance of the initial angle: Used to compare initial movement direction and movement vector.
6. Distance estimation: Assess the monkey's ability to estimate target distance from ICMS by regressing initial movement distance against target distance for ICMS-only trials, excluding trials for which the first movement segment was not the longest.

Evaluating Sensory Integration

Minimum variance integration, which is supposed to the optimal integration, predicts that in VIS+ICMS condition, as the visual coherence increases from 0% to 100%, the animals should transition from relying primarily on the ICMS cue to primarily on the visual cue -- under the model of minimum variance integration, each sensory cue should be wieghted inversely proportional to its variance.

Results

1. Monkey learns all three tasks.
2. VIS+ICMS outperforms VIS only for visual coherence less than 50%.
3. Optimal (minimum variance integration) integration of the two sensory modalities observed.

And only 8 electrodes!!

I can apply linear algebra, but often forget/confuse the spatial representations.

A good resource is Gilbert Strang's essay. I remember him talking about this when I took 18.06, but he was old at that point, and I barely went to class. So I didn't retain much. This notes of his still retains his stream of consciousness style, but the two diagrams summarizes it well, and is useful to often go back and make sure I still understand it.

The first one shows the relationship between the four subspaces of a matrix $A$. The second one adds in the relationship between the orthonormal basis of the subspaces.

Strang concludes:

Finally, the eigenvectors of $A$ lie in its column space and nullspace, not a natural pair. The dimensions of the spaces add to $n$, but the spaces are not orthogonal and they could even coincide. The better picture is the orthogonal one that leads to the SVD.

The first assertion is illuminating. Eigenvectors $v$ are defined such that $Av=\lambda v$. Suppose $A$ is $M\times N$, then $v$ must be $M\times 1$, therefore eigenvectors only work when $M=N$. On the other hand, in SVD, we have $A=U\mathrm{\Sigma }{V}^T$ and

• $A{v}_i={\sigma }_i{u}_i$ for $i=1,...,r$, where $r$ is the rank of column and row space.
  • $u_i$ are the basis for the column space (left singular vectors), $v_i$ are the basis for the row space (right singular vectors).
  • The dimensions for this equation matches because the column space and row space are more natural pair.
• $A{v}_i=0$, $A^T{u}_i=0$, for $i>r$.
  • $v_i$ are the eigenvectors of the null space of $A^T$,
  • $u_i$ are the eigenvectors of the null space of $A$.
  • They also match up similarly (Figure 2).
• In $Ax=b$, $x$ is in the row space, $b$ is in the column space.
• If $Ax=0$, then $x$ is in the null space (kernel) of A, and is orthogonal complement of the row space of A, $C(A^T)$.
• In $A^{T}x=b$, $x$ is in the column space, $b$ is in the row space.
• If $A^{T}x=0$, then $x$ is in the cokernel of A, and is orthogonal complement of the column space of A, $C(A)$.

Relationship with PCA

PCA Algorithm
Inputs: The centered data matrix $X$ and $k>1$.

1. Compute the SVD of $X$: $[U,\mathrm{\Gamma },V]=svd(X)$.

2. Let $V_k=[{\mathbf{v}}_1,...,{\mathbf{v}}_k]$ be the first $k$ columns of $V$.

3. The PCA-feature matrix and the reconstructed data are:

   $$Z=X{V}_k$$$$\hat{X}=X{V}_k{V}_k^T$$

So in PCA, the rows of the data matrix are the observations, and the columns are in the original coordinate system. The principle components are then the eigenvectors of the row space. We can do PCA in MATLAB with pca or manually with svd:

% PCA test
a = rand(100,1);
b = 5*a+rand(100,1);

data = [a, b];  % rows are observations
plot(a,b, '.');


% PCA results
% coeffs=PC in original coordinate[PxP], 
% scores=observation in PC-space [NxP], 
% latent=variance explained [Px1]
[coeffs, score, latent] = pca(data);
hold on;
plot(score(:,1), score(:,2), 'r.');

% SVD results
centeredData = bsxfun(@minus, data, mean(data,1));
[U, S, V] = svd(centeredData);
svd_score = centeredData*V;
plot(svd_score(:,1), svd_score(:,2), 'g.');

The results shown below. Blue is original data, green/red are the PCA results, they overlap exactly. Note that MATLAB's pca by default centers the data.

Projection into subspace (e.g. Kaufman 2014, Cortical activity in the null space, Even-Chen 2017, Neurally-driven error detectors)

Suppose we have a trial-averaged neural activity matrix $A$ of size $N\times T$, where $N$ is number of neurons, and $T$ is number of time bins.

In online BMI experiment, a linear decoder maps the neural activity vector $n_t$ of size $N\times 1$ to kinematics $v_t$ of size $2\times 1$ via the equation $v_t=w{n}_t$, where $w$ is of size $2\times N$.

Kaufman describes the output-potent neural activities as collection of $n_t$ such that $v_t$ is not null. Therefore the output-potent subspace of $n_t$ is the rowspace of $w$. Similarly, the output-null subspace is the null space of $w$.

By projecting the activity matrix $A$ into these subspaces, we can get an idea of how much variance in the neural activities can be accounted for the modulation to control actuator kinematics:

1. Use SVD on $w=U\mathrm{\Sigma }{V}^T$ to get its row and null space, defined by the first $r$ columns of $V$ (call it $w_{potent}$), and the last $N-r$ columsn of $V$ (call it $w_{null}$), respectively, where $r$ is the rank of $w$.
2. Left multiply $A$ by these subspaces (defined by the those columns) to get $A_{potent}$ and $A_{null}$.
3. The variance of $A$ explained by projection into the subspaces is obtained by first subtracting each row's mean from each matrix, then taking the L2 norm of the entire matrix (Frobenius norm of the matrix).

Philip Sabes' Linear Algebra notes

Wiener Filter

Wiener filter is used to produce an estimate of a target random process by LTI filtering of an observed noisy process, assuming known stationary siganl and noise spectra. This is done by minimizing the mean square error (MSE) between the estimated random process and the desired process.

Wiener filter is one of the first decoding algorithms used with success in BMI, used by Wessberg in 2000.

Derivations of Wiener filter are all over the place.

1. Many papers and classes refer to Haykin's Adaptive Filter Theory, a terrible book, in terms of setting the motivation, presenting intuition, and the horrible typesetting.

2. MIT's 6.011 notes on Wiener Filter has a good treatment of DT noncausal Wiener filter derivation, and includes some practical examples. Its treatment on Causual Wiener Filter, which is probably the most important regarding real-time processing, is mathematical and really obscures the intuition -- we reach this equation from completing the square and using Parseval's theorem, without mentioning the consquences in the time domain. My notes

3. Max Kamenetsky's EE264 notes gives the best derivation and numerical examples of the subject for practical application, even though only DT is considered. It might get taken down, so extra copy [here](/reading_list/assets/wienerFilter.pdf}. Introducing the causual form of Wiener filter using input whitening method developed by Shannon and Bode fits into the general framework of Wiener filter nicely.

Wiener Filter Derivation Summary

1. Both the input $\mathbf{x}$ (observation of the target process) and output $\mathbf{y}$(estimate of the target process $\mathbf{d}$, after filtering) are random processes.

2. Derive expression for cross-correlation between input and output.

3. Derive expression for the MSE between the output and the target process.

4. Minimize expression and obtain the transfer function in terms of ${\mathbf{S}}_{\mathbf{xx}}$ and ${\mathbf{S}}_{\mathbf{xd}}$, where $\mathbf{S}$ are Z or Laplace transforms of the cross-correlations.

This looks strangely similar to a linear regression. Not surprisingly, it is known to statisticians as the multivariate linear regression.

Kalman Filter

In Wiener Filter, it is assumed that both the input and target processes are WSS. If not, one may assume local stationarity and conduct the filtering. However, nearly two decades after Wiener's work, Rudolf Kalman developed the Kalman filter, which is the optimu mean square linear filter for nonstationary processes (evolving under a certain state space model) AND stationary ones (converging in steady state to Wiener filter).

Two good sources on Kalman Filter:

1. Dan Simon's article describes the intuition and practical implementation of KF, specifically in an embedded control context. The KF should be coupled with a controller when the sensor reading is unreliable -- it filters out the sensor noise. My notes

   

2. Greg Welch and Gary Bishop's An Introduction to the Kalman Filter. Presents just the right amount of math in the derivation of the KF. My notes

3. Update (12/9/2021): New best Kalman Filter derivation, by Thacker and Lacey. Full memo, Different link.

The general framework of the Kalman filter is (using notation from Welch and Bishop):

The first equation is the state model. $x_k$ denotes the state of a system, this could be the velocity or position of a vehicle, or the desired velocity or position of a cursor in BMI experiment. $A$ is the transition matrix -- describes how the state will transition depending on past states. $u_k$ is the input to the system. $B$ describes how the inputs are coupled into the state. $w_k$ is the process noise.

The second equation is the observation model - it describes what kind of measurements we can observe from a system with some state. $z_k$ is the measurement, it could be the speedometer reading of the car (velocity would be the state in this case), or it could be neural firing rates in BMI (kinematics would be the state). $H$ is the observation matrix (tuning model in BMI applications). $v_k$ is the measurement or sensor noise.

One caveat is that both $w$ and $v$ are assumed to be Gaussian with zero mean.

The central insight with Kalman filter is that, depending on whether the process noise or sensor noise dominates, we weigh the state model and observation model differently in their contributions to compute the new underlying state, resulting in a posteriori state estimate \[\hat{x_k}=\hat{x_k}^- + K_k(z_k-H\hat{x}_k^-)\] Note the subscript ${}_k$ denotes at each discrete time step.

The first term ${\widehat{x_k}}^{-}$ is the contribution from the state model - it is the a priori state estimate based on the state model only. The second term is the contribution from the observation model - given the a posteriori state estimate.

Note a priori denotes a state estimate at a given time state $k$ to use only knowledge of the process prior to step $k$. a posteriori denotes a state estimate that also uses the measurement at step $k$, $z_k$.

Last september I went through Caltech's Learning from Data course offered through EdX. Went through all the lectures and homework except for the final exam.

Finally got around to finish it this week, after re-reading some forgotten materials. All the code written for the problem sets are here. Some notes:

VC Dimension and Generalization

One of the most emphasized point in the course, is how to estimate the generalization performance of an algorithm. VC-Dimension can be used as a preliminary measure of an algorithm's generalization performance. A more complex hypothesis is more likely to overfit, and given the same amount of training data, may lead to worse generalization. When possible, using simpler hypothesis set is better. Otherwise, use regularization.

Linear Regression

Simple, not very sexy, but surprisingly powerful in many applications. Combined with nonlinear transforms can solve many classes of problems. We have many techniques that can solve linear problems. So in general, want to try to reduce problems into this class.

Validation

Cross-validation, especially leave-one-out, is an unbiased estimator of the out of sample error $E_{out}$.

Use validation for model selection, including parameters for regularization.

SVM

Very powerful technique. Motivation is simple - finding a hyperplane that separats two classes of data with the greatest margin from the separation plane to the closest points of each class. Solving the equations become a quadratic programming problem of minimizing the norm of the weights of the plane (which is inversely proportional to the margin width), subject to the all points being classified correctly (in hard-margin SVM).

This original formulation is called the primal problem.

The same problem can be formulated into a LaGarange Multiplier problem, with an additional multiplier parameter ${\alpha }_i$ for each data point. This problem then requires the minimizing over the weights, after maximizing over the multiplier $\alpha$s. Under the KKT conditions (or vice versa), we can switch the order to maximizing over the multipliers after minimizing over the weights. This allows us to write expressions for the weights in terms of $\alpha$ after doing the minimization (by taking the partial derivatives of the expression).

Finally, we reach another Quadratic-Programming problem, where the objective is over $\alpha$s, subjective to constraints from the weights' minimization.

The advantages of this Dual Problem is that the data points are present in the expression in terms of inner products -- allowing us to use the kernel trick, which is a computationally efficient way of doing nonlinear transformation to higher-order (even infinite) dimensions.

One of the coolest thing about SVM is that, according to strict VC-dimension analysis, after nonlinear transformation of the data points into infinite dimensions via the kernel trick, $E_{out}$ should be unbounded. However, because SVM searches for hyperplane with the fattest separation margin, the effective VC-dimension is significantly reduced, and thus $E_{out}$ is under control.

RBF

RBF network classifiers places a RBF on each training data point, and then classifies test points by summing those RBF values at the test point.

Since this is prohibitive when data set is big, we can instead pick K representative points, by finding the centroid of K clusters (via clustering algorithm). Therefore, the classification problem is transformed into a linear regression problem, where the basis are the RBF centered around the cluster centers.

SVM with RBF kernel still outperforms the regular-RBF network classifiers most of the time. Why do we use it? I can imagine doing unsupervised learning: have a cluster of data points with no labels, but simply use clustering + RBF to derive K labels and assign them to new samples.

Results of the comparison in terms of the metrics given in the metrics post.

Right click to open plots in a new window to see better

Victor Purpura

In this plot, the x-axis is the acceptable time shift we can shift a spike in the recording to match one in the reference, and equal to $1/q$, where $q$ is the shift-cost in the original VP formulation.

When the acceptable time shift is small, VP is a measure of the number of non-coincident spikes. When the shift is large, it is more a measure of difference in spike counts.

As expected, the performance is much worse when SNR is low. As expected, Plexon performs well on the VP metric across all timescales. RHD has very close performance, except in the 10ms scale. This is most likely due to the onboard spike-sorting uses only 0.5ms window rather than the full 1ms window used in Plexon, resulting in missed spikes or shifted spike times. I expect the difference between plexon and RHD to decrease with shorter spike duration/features.

RHA has the worst performance, and this is especially apparent for low SNR recordings. The difference of the performance difference between RHA and RHD is most likely RHA's use of AGC. When SNR is low, AGC also amplifies the noise level - therefore a burst in noise may result in amplitude similar to a spike. This is also apparent when trying to align the RHA and reference waveforms prior to metric comparison - with simple peakfinding it is impossible to align the signals properly when SNR=1dB. More advanced frequency-domain techniques may be needed. Therefore, the cyan RHA curve should be counted as an outlier.

The mean and standard deviation plot confirms the above. At time scales greater than 10ms, plexon and RHD have very close performance over different SNRs.

van Rossum

The x-axis is the $\tau$ parameter used in the exponential kernel. As $\tau$ increases, the metric is supposed to measure non-coincident spikes to difference in spike counts and firing rate.

I would expect the curves to show the same trend as that in the VP distance. But instead it shows the opposite trend. Further, the results don't agree with the other tests...therefore I must conclude even the corrected Paiva formula is incorrect..?

Schreiber

The x-axis is the $\sigma$ parameter used in the Gaussian kernel. As $\sigma$ increases, the metric measures the non-coincident spikes to difference in spike counts and firing rates. The curves show the expected shape. And again, at time scale greater than 10ms, all three systems have simlar performance.

Binned Distance

The x-axis is the bin size used in calculating the binned distance. The order of the curves are almost the same as that in the VP-distance. Again, Plexon performs the best for small time scale, all three systems converge in performrance with increasing bin size.

The mean curve shows the convergence for binned distance is a lot steeper than that for VP-distance. This is really good news, as most of our decoding algorithms use binned firing rates. It shows for bin size $>=25ms$, the wireless systems have performarnce very close to Plexon.

Finally, the order of performrance is again $plexon>RHD>RHA$.

Some computation problems/notes I encountered while implementing the metrics. Code

Victor Purpura Distance

Victor-Purpura's MATLAB implementation, adapted from the Seller algorithm of DNA sequence matching, while having $O(N_i{N}_j)$ performance runs pretty slow.

For a test comparison of two spike trains, one with 8418 spike times and the other with 9782 spike times, it takes around 75 seconds. A bit too long. On Victor's page, there are a few other Matlab implementations, but only deal with parallelizing calculations with different cost of shifting a spike. The mex function has weird usage. So I tried translating the algorithm into Julia and calling it from Matlab. The result is spkd_qpara.jl:

Pretty straight forward. Importing my spike time vectors into Julia and running the function, it takes about 1.07 seconds, a significant speed-up. However, most of my analysis, plotting, and data are in Matlab, so I would like to call Julia from Matlab. This functionality is provided by jlcall.

Configuration through running jlconfig as instructed in the README was smooth, except for the message:

> Warning: Unable to save path to file '/usr/local/MATLAB/R2015a/toolbox/local/pathdef.m'. You can save your path to a different location by calling SAVEPATH with an input argument that specifies the full path. For MATLAB to use that path in future sessions, save the path to 'pathdef.m' in your MATLAB startup folder. 
> > In savepath (line 169)
>   In jlconfig (line 100) 

Warning most likely related to my machine.

Using any methods from Jl.m, however, was not. I received the error:
Invalid MEX-file '/home/allenyin/.julia/v0.4/jlcall/m/jlcall.mexa64': libjulia.so: cannot open shared object file: No such file or directory.

So it seems Matlab cannot find the libjulia.so. This is documented jlcall's bug list.

Simple fix is as suggested in the message thread: in Matlab do
setenv('LD_RUN_PATH', [getenv('LD_RUN_PATH'), ':', '/usr/lib/x86_64-linux-gnu/julia')
before running the jlconfig script. The path given is the location of the so file.

Now to call victorD from Matlab, do:

Jl.include(`spkd_qpara.jl');
Jl.call('victorD', spikeTimes1, spikeTimes2, 200);

The second call takes 1.41 seconds.

Van Rossum Distance

Paiva 2009 derived a computational effective estimator with order $O(N_i{N}_j)$ for the VR-distance:

where $L_{\tau }(\cdot )=exp(-abs(\cdot )/\tau )$ is the Laplacian kernel. However, this formula is wrong. By inspection we can see that this distance will never be 0 since it is a sum of exponentials. Further sample calculation for distance between less similar spike trains may even yield smaller distance! These problems can be corrected by changing the sign of the last summation term. Unfortunately, this typo occurs in (Paiva et al., 2007) as well as Paiva's PhD thesis. However, as I can't derive the formula myself (there must be some autocorrelation trick I'm missing), I don't trust it very much.

It is nevertheless, a much more efficient estimator than the naive way of taking the distance between convolved spike trains, and does not depend on time discretization.

Thomas Kreuz has multiple van Rossum Matlab code posted on his website, but they don't work when $\tau <20ms$.

Schreiber Distance

This dissimilarity measure also have a data-effective method of $O(N_i{N}_j)$, given in Paiva 2010.

Generating Test Signals

Signals were generated using Leslie Smith and Nhamoinesu Mtetwa's Noisy Spike Generator MATLAB Software v1.1 (NSG) using makeReferenceSignals.m.

Sampling rate was set to 31250Hz since that is the sample rate of the wireless headstages. This frequency is greater than the maximum Plexon ADC frequency of 20,000Hz, but offline analysis may simply use interpolation.

Notes on using this toolbox:

1. The main script generatenoisysamples.m outputs a final signal that includes noise from uncorrelated spike noise, correlated spike noise, and Gaussian noise. The NoiseSNR only sets the Gaussian noise level. As this validation is on recording quality, not spike sorting algorithm, I modified that script to not include the uncorrelated and correlated spike noise in the final output.

2. While the manual of the toolbox claims that the spike duration can be changed by changing the T_Delta_Integrate and N_Delta_integrate parameters (spike duration is T_Delta_Integrate X N_Delta_Integrate). However, changing these parameters simply changes how many samples it takes from a pre-generated template file. These template files were generated by the author and the script used was not available. Regardless, the default spike duration of ~1.8ms, while longer than most motor cortex spikes we encounter, can still be sorted and detected by all three systems teseted.

Aligning Reference with Recording

After the reference signals are generated, they are converted to .wav files with Fs=31250Hz. All audio signals (including those with two distinct spikes firing) are available on soundcloud. The audio signals then goes through the Plexon headstage test board, to which the wireless and plexon headstage may connect.

As mentioned in Validation of signal quality I, since the reference signal and the recording cannot be started and stopped at exactly the same time, some alignment needed to be done before applying the spike train measurements.

The reference and recording are aligned in the start by aligning the peak of the first spike in the reference with that of the recording. I use the recorded analog waveform, rather than the recorded spike times for alignment because the first spike may not be detected, and it's easier to examine the alignment quality visually from the analog waveforms.

The first spike peak of the reference signal is easily found by doing peak-finding on a 5ms window after the first spike-time (which is known). The spike times generated by NSG marks the beginning of a spike, not the peak.

When SNR is high, peak-finding on the recording can also find the peak of the first recorded spike pretty easily. But with lower SNR, the noise level gets higher and the MinPeakHeight parameter of MATLAB's findpeaks() must be adjusted so that a noise peak is not being mistaken for a signal peak. Of course, it's not always possible to align two signals, contributing to bad spike train comparison. The best MinPeakHeight for found this way for each recorded signal is in compare_signals.m. The script checkAlignment.m helps with that.

For the end of the recording signal - sometimes when I don't stop the input audio signal in time, extra signal is recorded. Thus after alignment, I cut the recording to within 102 seconds of the alignment start.