A very cool paper from the Williams lab at Harvard-MGH came out this month: Semantic encoding during language comprehension at single-cell resolution.

It records from 10 awake neurosurgery patients from the superior posterior middle frontal gyrus within the dorsal prefrontal cortex of the language-dominant hemisphere, while they listened to different short sentences. Comprehension was confirmed by asking follow-up questions to the sentences. 133 well-isolated units from the 10 patients were collectively analyzed.

The results are very satisfying. Also see nature commentary on this paper.

Semantic tuning

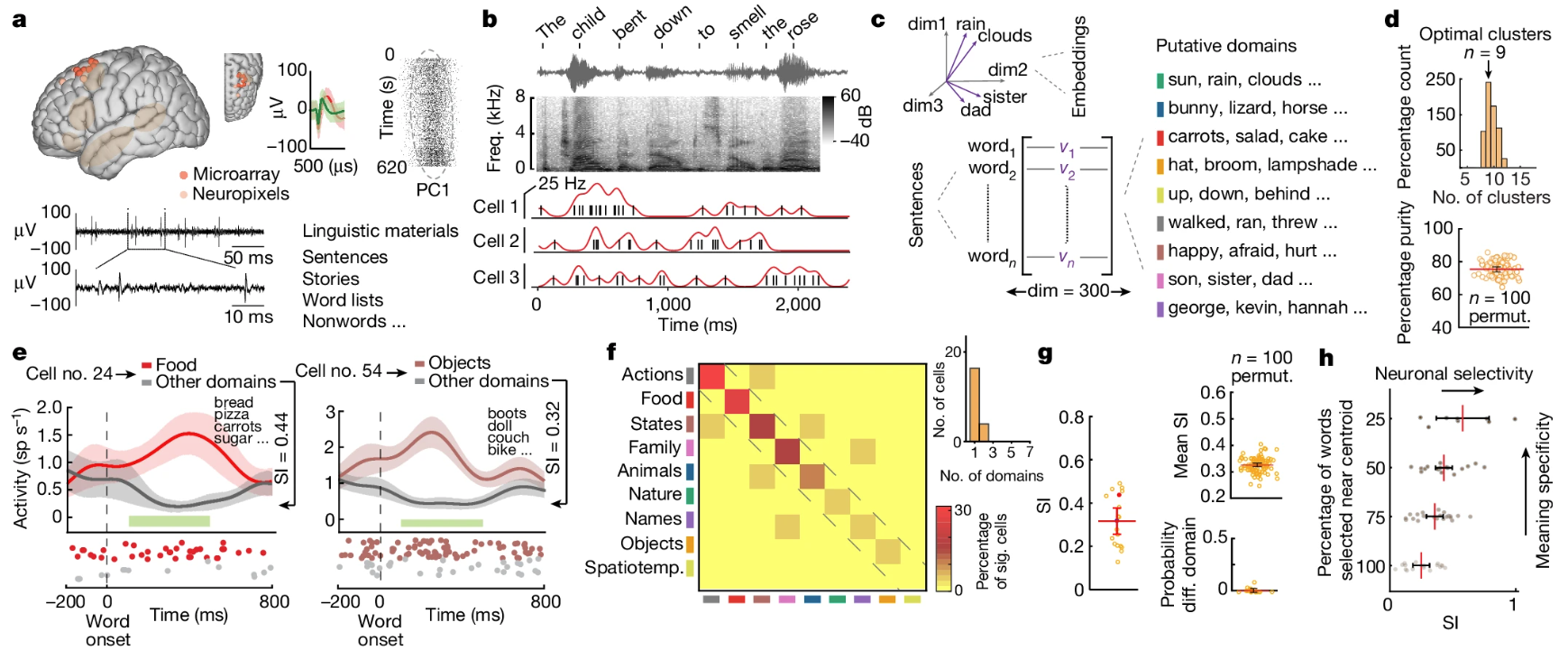
They found something akin to “semantic tuning” on the single neuron level to the words in the sentence.

• This is done by correlating neuron firings to the semantic content of each word in time, where the semantic content of a word is a multi-dimensional embedding vector (derived from models like word2vec).
• A neuron is tuned to a “semantic domain” if its firing rate is significantly higher for that domain vs. others.
• They observed most of the neurons exhibited semantic selectivity to only one semantic domain. Though construction of 1-vs-all determination of semantic tuning this conclusion is a bit weak.
• As a control, many semantic-selective neurons also distinguished real vs. non-words.

Generalizable semantic selectivity

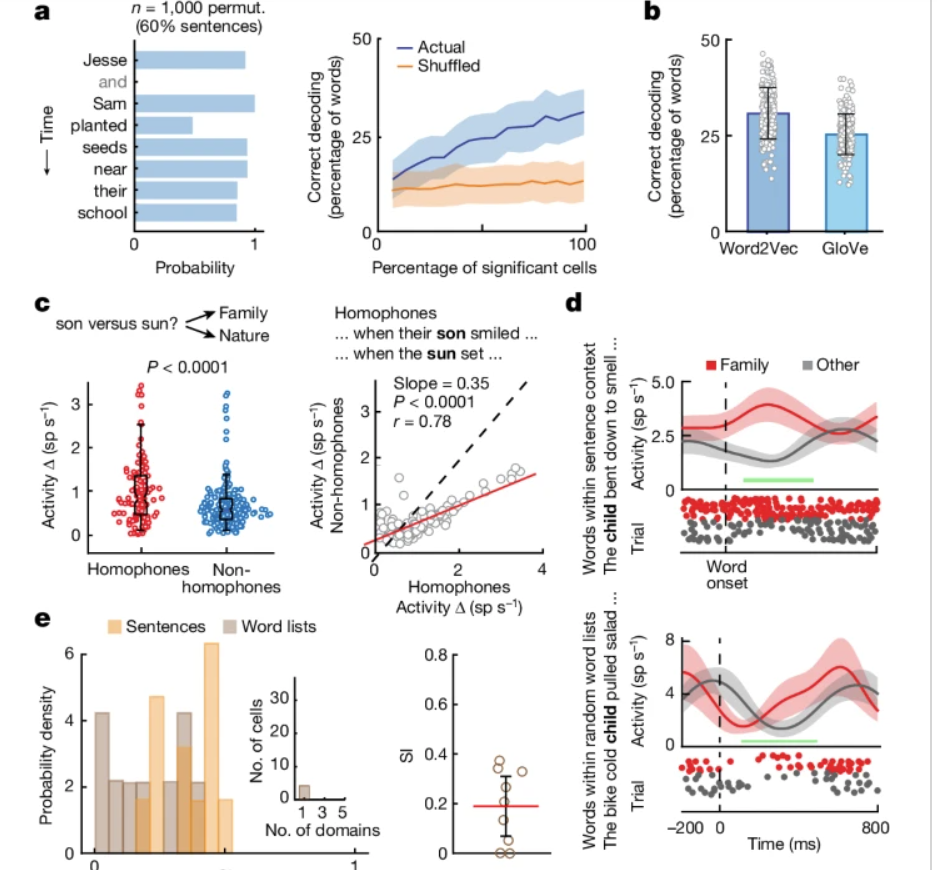
• Semantic decoders generalize to words not used in the training set (31+/-7%)
• Semantic decoders work when a different word-embedding model is used (25+/-5%)
• Decoding performance holds regardless of position in a sentence (23% vs 29%)
• Works for multi-unit activities (25%)

Considering they use a support vector classifier with only 43 neurons, this is really good.

Additional control found different story “narrative” (different thematic and style) does not affect semantic decoding (28% accuracy using decoders trained from a different narrative).

The decoding experiments used the response from the collective semantically-tuned neurons from all 10 participants (they can do this since the tasks are the same across participant). They checked the semantic decoding generalizability hold for individual participant.

Context-dependence

• Presenting words without context yield much lower semantic-selectivity from the units compared to when they were presented in a sentence.
• Homophone pairs (words that sound the same but mean different things) showed bigger differences in semantic-selective units compared to non-homophone pairs (words that sound different but semantically similar).
• Context helped with semantic decoding
  • They assigned a “surprisal”-metric to each word using a LSTM: high surprisal means based on the context, the prob that a word is surprising;
  • They looked at the decoding performance as a function of surprisal
  • Decoding performance for low-surprisal words significantly higher than for high-surprisal words

Neural representation of the semantic space

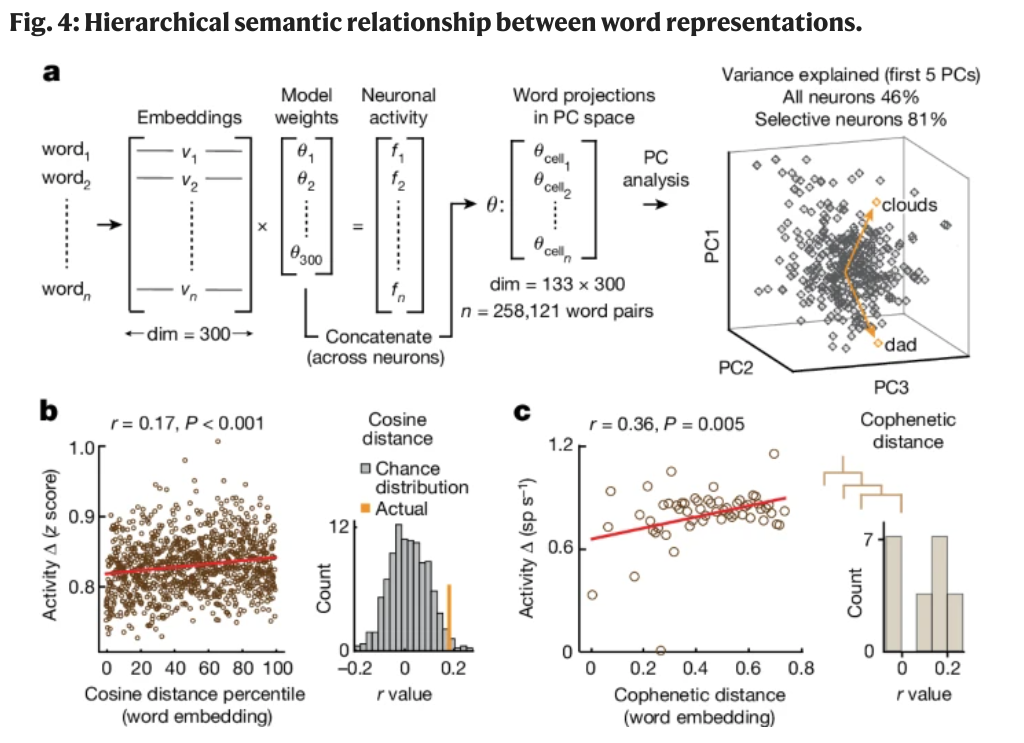
Even though a neuron might be selective primarily to a single semantic domain, the actual semantic representation could be distrbuted (perhaps in a sparse manner). Statistical significance from permutation tests.

They regressed the responses of all 133 units onto the embedding vectors (300-dimensional) of all words in the study.

• This results in a set of model weights for each neuron (i.e. how much each neuron encodes a particular semantic dimension)
• The concatenated set of model weights is then a neural represention of the semantic space (neurons-by-embeddings, 133x300 in this case).
• Top 5 PC accounts for 81% of activities of semantically-selective neurons.
• Different in neuronal activities correlated with word-vector distance (measured with cosine similarity). r=0.17
• Word pairs with less hierarchical semantic distance (cophenetic distance) elicited more similar neuronal activities, r=0.36.

These last two points are interesting. It FEELS right, since hierarchical semantic organization probably allows a moer efficient coding scheme for a large and expanding semantic space.

Impact

This work is spiritually similar to the Huth/Gallant approaches for looking at fMRI during story-listening to examine language processing. But the detailed single-neuron results make it reminiscent of the classic Georgeopoulos motor control papers that largely formed the basis of BMI (1, 2).

While the decoding accuracy (0.2-0.3) here is looks much lower than the initial motor cortex decoding of arm trajectories in the early papers, it is VERY GOOD considering the much higher dimensionality of the semantic space. While the results might not be too surprising – we know semantic processing has to happy SOMEWHERE in the brain, it is surpising how elegant the results here are.

The natural next-step IMO is to obviously recorded from more neurons with more sentences, etc. I would then love to see:

1. Fine-tune LLM with the recordings: since the neural activities are correlated with semantic content, it could be projected into a language model’s embedding space.
2. Try to reconstruct sentences’ semantic meaning, and the LLM can be additionally be used to sample from the embedding space for sentence “visualization”.

And this will be a huge step toward what most people perceive as “thought”-decoding vs. speech-decoding (which deals more with the mechanics of speech roduction such as tones and frequencies vs. languag aspects such as semantics).

What else are needed?

The discussion section of the paper is a good read, and this section stands out regarding different aspects of semantic processing:

Modality-dependence

As the present findings focus on auditory language processing, however, it is also interesting to speculate whether these semantic representations may be modality independent, generalizing to reading comprehension, or even generalize to non-linguistic stimuli, such as pictures or videos or nonspeech sounds.

Production vs. Comprehension

It remains to be discovered whether similar semantic representations would be observed across languages, including in bilingual speakers, and whether accessing word meanings in language comprehension and production would elicit similar responses (for example, whether the representations would be similar when participants understand the word ‘sun’ versus produce the word ‘sun’).

Perhaps the most relevant aspect to semantic-readout. It’s unclear whether semantic processing in production of language (as close to thoughts as we can currently define) is similar to that during comprehension. Although a publication from the same group examines speech production (phoneme, syllables, etc) in the same brain region (the second paper says posterior middle frontal gyrus of the langauge-dominant prefrontal cortex, illustration looks similar), examined the organization of the cortical column and saw their activities transitioned from articulation planning to production.

It would be great to know if the semantic selectivity holds during speech production as well – the combined findings suggest there’s a high likelihood.

Cortical Distribution

It is also unknown whether similar semantic selectivity is present across other parts of the brain such as the temporal cortex, how finer-grained distinctions are represented, and how representations of specific words are composed into phrase- and sentence-level meanings.

Language and speech neuroscience has evolved quickly in the past two decades, with the traditional thesis that Broca’s area is responsible for language production being challenged with more evidence implicating the role of precentral gyrus/premotor cortex.

Meanwhile the hypothesis that Werneke’s area (posterior temporal lobe) for language understanding has withstood more test of time. How this is connected to the semantic processing observed in this paper in prefront gyrus should (e.g. is it downstream or upstream in language production) certainly be addressed.

My (hopeful) hypothesis is that the prefrontal gyrus area here participates in both semantic understanding and production. I don’t believe this as far-fetched given how motor/premotor cortex’ roles in both action observation and production in the decades of BMI studies.

Paper link

This paper advances the SOTA on silent-speech decoding from EMG recorded on the face. “Silent” here means “vocalized” or “mimed” speech. The dataset comes from Gaddy 2022.

Image above shows the overall flow of the work:

1. Model is trained to align EMG (from vocalized and silent) and audio into a shared latent space from which text-decoding can be trained. This training utilizes some new technique they call “cross-modal contrastive loss” (crossCon) and “supervised temporal contrastive loss” (supTCon). More on this later.
2. They take the 10 best models trained with different loss and data-set settings, and make into an ensemble.
3. For inference, they get the decoded beam-search output from these different models, and pass them into a fine-tuned LLM, to infer the best text transcription. They call this LLM-based decoding “LLM Integrated Scoring Adjustment” (LISA).

Datasets

The Gaddy 2022 dataset contains:

1. EMG, Audio, and Text recorded simulataneously during vocalized speech
2. EMG and Text for silent speech
3. Librispeech: Synchronized Audio + Text

Techniques

A key challenge to decode silent speech from EMG is the lack of labeled data. So a variety of techniques are used to overcome this, drawing inspiration from self-supervised learning techniques that have advanced automatic-speech recognition (ASR) recently.

Cross-modality Contrastive Loss (crossCon): Aims to make cross-modality embeddings at the same time point more similar than all other pairs. This is really the same as CLIP-style loss.

Supervised temporal contrastive Loss (supTCon): This loss aims to leverage un-synchronized temporal data by maximizing similarity between data at time points with the same label than other pairs.

Dynamic time warping (DTW): To apply crossCon and supTCon to silent speech and audio data, it’s important to have labels for the silent speech EMG. DTW leverages the fact that vocalized EMG and audio are synchronized, by:

1. Use DTW to align vocalized and silent EMG
2. Pair the aligned silent EMG with the vocalized audio embeddings.

Using audio-text data: To further increase the amount of training data, Librispeech is used. Since the final output is text, this results in more training data for the audio encoder, as well as the joint-embedding-to-text path.

All these tricks together maximize the amount of training data available for the models. I think there are some implicity assumptions here:

1. EMG and Audio have more similarity with EMG and Text, since both Audio and EMG have temporal relationship.

The use of a joint-embedding space between EMG and Audio is crucial, as it allows for different ways to utilize available data.

LISA: An LLM (GPT3.5 or GPT4) are fine-tuned on the EMG/Audio-to-Text outputs for the ensemble models, and the ground truth text transcriptions. This is done from the validation dataset. Using LLM to output the final text transcription (given engineered prompt and beam-search paths), instead of the typical beam-search method, yielded significant improvements. And this technique can replace other language-model based speech-decoding (e.g. on invasive speech-decoder output) as well!

Details:

1. CrossCon + DTW performed the best. It’s interesting to note that DTW with longer time-steps (10ms per timepoint) perform better.
2. SupTCon loss didn’t actually help.
3. Mini-batch balancing: Each minibatch has at least one Gaddy-silent sample. Vocalized Gaddy samples are class-balanced with Gaddy-silent sample. The rest of the mini-batch is sub-sampled from Librispeech. This is important to ensure the different encoders are jointly optimized.
4. GeLU is used instead of ReLU for improved numerical stability.
5. The final loss function equals to weighted sum EMG-CTC_loss, Audio-CTC_loss, CrossCon and supTConLoss

Final Results on Word-Error Rate (WER)

For final MONA LISA performance (joint-model + LLM output):

1. SOTA on Gaddy silent speech: 28.8% to 12.2%
2. SOTA on vocal EMG speech: 23.3% to 3.7%
3. SOTA on Brain-to-Text: 9.8% to 8.9%

Additional userful reference

Cites Acceptability of Speech and Silent Speech Input Methods in Private and Public:

The performance threshold for SSIs to become a viable alternative to existing automatic speech recognition (ASR) systems is approximately 15% WER

Neurips 2023 has been incredibly awesome to scan through. The paper list is long and behind paywall, but usually searching for the paper titles will bring something up in arxiv or some tweet-thread related to it.

Patrick Mineault (OG Building 8 ) has collected a list of NeuroAI papers from Neurips which has been very useful to scan through.

Quirky papers

Time Series as Images: Vision Transformer for Irregularly Sampled Time Series

Instead of trying to figure out how to align differently sampled time series for time series classification task, plot them and send the image form to vision transformer, add a linear prediction head on top and be done with it.

And this actually works:

We conduct a comprehensive investigation and validation of the proposed approach, ViTST, which has demonstrated its superior performance over state-of-the-art (SoTA) methods specifically designed for irregularly sampled time series. Specifically, ViTST exceeded prior SoTA by 2.2% and 0.7% in absolute AUROC points, and 1.3% and 2.9% in absolute AUPRC points for healthcare datasets P19 [29] and P12 [12], respectively. For the human activity dataset, PAM [28], we observed improvements of 7.3% in accuracy, 6.3% in precision, 6.2% in recall, and 6.7% in F1 score (absolute points) over existing SoTA methods.

Even though most of the “plot” image is simply empty space, attention map shows the transformer is attending the actual lines, and regions with more changes.

Why does this work? I’d think it’s because the ViTST acts as an excellent feature extractor, since the DL vision models contains in them representations of primitive features typically present in the line signals (e.g. edges, curves, etc). Yet using a pretrained ResNet showed much worse performance vs. the pretrained SWIN-transformer (but still higher than the trained-from-scratch SWIN-transformer). That suggests transformer’s cross-attention between different time series (or different regions of the plot) might make a difference.

Should we use it? Probably not – lots of compute and memory is being wasted here producing mostly empty pixels. But it’s a sign of the coming trend of leverage pre-trained model or die trying.

Training with heterogenous multi-modal data

Data collection sucks and everyone knows it, especially neuroscientists. How we wish we can just bust out some kind of Imagenet, CIFAR, or COCO like the vision people? Nope, datasets are always too heterogenous in sensors, protocols, or modalities. Transformers are now making it easier to combine them now though (see for example previous).

BIOT: Biosignal Transformer for Cross-data Learning in the Wild

Main contributions:

• Biosignal transformer (BIOT): a generic biosignal learning model BIOT by tokenizing biosignals of various formats into unified “sentences.” •
• Knowledge transfer across different data: BIOT can enable joint (pre-)training and knowledge transfer across different biosignal datasets in the wild, which could inspire the research of large foundation models for biosignals.
• Strong empirical performance. We evaluate our BIOT on several unsupervised and supervised EEG, ECG, and human sensory datasets. Results show that BIOT outperforms baseline models and can utilize the models pre-trained on similar data of other formats to benefit the current task.

Fancy word aside, the main takeways:

1. Segment time series into 1s chunks (called tokens). Then parametrize with 3 embeddings: [channels, samples] –> [(dim_emb1 + dim_emb2 + dim_emb3),].
2. Pass them through a linear transformer (use reduced-rank form of self-attention).
3. Profit with transformer embedding outputs..

This is very similar approach to Poyo1, which uses relative position embedding and does not need to explicitly chunk 1s windows.

Interestingly, BIOT paper claims to be “the first multi-channel time series learning model that can handle biosignals of various formats”. And both BIOT and POYO1 are in the Neurips 2023.

Leveraging LLM for decoding

Continuing onto the trend of using LLM at the end of all the ML stacks.. such as decoding mental image by conditioning diffusion models on fMRI, now we can decode “language” from EEG much better.

DeWave: Discrete Encoding of EEG Waves for EEG to Text Translation

Context:

Press releases such as this one would have you believe they have “developed a portable, non-invasive system that can decode silent thoughts and turn them into text”.

But what exactly are the “silent thoughts”?

study participants silently read passages of text while wearing a cap that recorded electrical brain activity through their scalp using an electroencephalogram (EEG)

This is different from what we typically think of “thoughts”, it’s more similar to decoding movies from neural activities (similar to Alexander Huth and Joe Culver works). Now we continue:

Main contributions:

• This paper introduces discrete codex encoding to EEG waves and proposes a new framework, DeWave, for open vocabulary EEG-to-Text translation.
• By utilizing discrete codex, DeWave is the first work to realize the raw EEG wave-to-text translation, where a self-supervised wave encoding model and contrastive learning-based EEG-to-text alignment are introduced to improve the coding ability.
• Experimental results suggest the DeWave reaches SOTA performance on EEG translation, where it achieves 41.35 BLUE-1 and 33.71 Rouge-1, which outperforms the previous baselines by 3.06% and 6.34% respectively

The paper does decoding with/without training data markers indicating where the subject’s looking at. The case without markers is much more interesting and sidesteps the labeling problem.

The overall approach:

1. Use a conformer to vectorize the EEG signals into embeddings,
2. the embeddings are mapped to a set of discrete “symbols” (or code) via a learned “codex”,
3. The codex representations are fed into pre-trained BART (BERT+GPT) and get the output hidden states. A fully connected layer is applied on the hidden states to generate English tokens from pre-trained BART vocabulary V.

It’s hard to decipher some of the details of this paper, but recording notes here for future me.

Training paradigm:

• In the first stage, they do not involve the language model in weight updates. The target of the first stage is to train a proper encoder projection to theta_codex and a discrete codex representation C for the language model.
• In the second stage, the gradient of all weights, including language model theta_BART is opened to fine-tune the whole system.

The codex approach is very interesting – instead of feeding EEG embeddings directly to the pre-trained BART, it gets converted into this intermediate representation. The rationale given was this:

It is widely accepted that EEG features have a strong data distribution variance across different human subjects. Meanwhile, the datasets can only have samples from a few human subjects due to the expense of data collection. This severely weakened the generalized ability of EEG-based deep learning models. By introducing discrete encoding, we could alleviate the input variance to a large degree as the encoding is based on checking the nearest neighbor in the codex book. The codex contains fewer time-wise properties which could alleviate the order mismatch between event markers (eye fixations) and language outputs.

Need temporal alignment between segments of signals and word (or “label”?).

Not sure if this is back-rationalization, but the training supports it:

To train the encoder as well as the codex, two self-supervised approach was used:

1. Encoder-decoder Reconstruction: raw waves -> embeddings -> codex -> embeddings -> raw waves. Notably subsequent ablation studies showed that a larger codex size is not necessarily better, which makes sense here as we expect a lower-D latent space for this approach to work.
2. Language (word2vec embeddings) and codex alignment via contrastive learning (of course!)

And this approach works, even though EEG is traditionally very shitty. Sure they used new graphene-based dry electrodes which supposedly approach wet-gel electrode performance, it’s still surprising. Though I’m not versed in EEG to understand how significant the outperformance margin vs. SOTA is.

I don’t buy the jusification for the codex representation though, as the abolation study shows the effect codex on word level EEG feature as minimal.

Predicting brain responses with large pre-trained models

Alex Huth is making it rain in Neurips this year with a series of fMRI response encoding papers, involving language and vision/video. One that stood out the most to me was Scaling laws for language encoding models in fMRI, also see tweet-thread.

Takeaways:

• Predicting fMRI brain response to story-listening with LLM: Brain prediction performance scales logarithmically with model size from 125M to 30B parameter models, with ~15% increased encoding performance as measured by correlation with a held-out test set across 3 subjects. Similar logarithmic behavior was observed when scaling the size of the fMRI training set.
• Similar trend exists for acoustic encoding models that use HuBERT, WavLM, and Whisper.

A noise ceiling analysis of these large, high-performance encoding models showed that performance is nearing the theoretical maximum for brain areas such as the precuneus and higher auditory cortex. These results suggest that increasing scale in both models and data will yield incredibly effective models of language processing in the brain, enabling better scientific understanding as well as applications such as decoding.

On the surprising effectiveness of neural decoding with large pre-trained models..

Deep-learning models were only “weakly” inspired by the brain and even though the Transformer arch isn’t exactly neuro-inspired, decoding and neural responses using large pre-trained models have been surprisingly effective and “straight-forward”.

My take is that these large pre-trained models (language, vision, audio, etc) encode structure of that particular modality. Brains proces these modalities differently from these models, but presumably there’s some kind of latent space that both can be mapped onto. So this stype of encoder-decoder approach can be thought of as latent space alignment (which can include temporal dimension as well!)

This is a step up from other dynamic-programming style alignment techniques such as viterbi decoding and CTC-loss, and much more elegant conceptually.

I remember spending an afternoon understanding the theoretical and pratical differences between PCA and FA several years ago, when factor analysis (FA) started to appear more frequently in neuroscience and BMI literature. It was confusing because it seemingly measured the same thing as the popular tool principal component analysis (PCA), but in a much more computationally complex way. When I tried FA on the neural data I was working on at the moment, I didn’t see much difference – reconstruction using the top-n PC components and the assumed n common factors accounted for similar amount of variance in the data.

Reading the recent paper relating neuronal pairwise correlations and dimensionality reduction made me double back on this again – the motivation question was can we derive similar results using PCA? The answer was no, and looking into this deepened my understanding of these two tools.

Problem Formulation

Both PCA and FA seek to provide a low-rank approximation of a given covariance (or correlation) matrix. “Low-rank” means that only a limited number of principal components or latent factors is used. If we have a \(n\times n\) covariance matrix of the data \(\mathbf{C}\), then we have the following model formulations:

Here \(\mathbf{W}\) is a matrix with \(k\) columns (\(k < n\)), representing the low number of principal components or latent factors, \(\mathbf{I}\) is identify matrix, and \(\mathbf{\Psi}\) is a diagnal matrix. Each method can be formulated as finding \(\mathbf{WW}\) (in FA’s case, als \(\mathbf{\Psi}\)) to minimize the norm of the difference between left-hand and right-hand sides.

Note that PPCA can be thought of as an intermediate between PCA and FA, where the noise term \(\sigma^2\mathbf{I}\) makes it a generative model like FA, it practically acts like PCA (in that \(\mathbf{W}\) spans the same subspace in both).

Difference in model assumptions

The principal components of PCA are derived from a linear combination of the feature vectors, akin to rotation (and scaling) of the feature-space. The directions of the PC are those where variance is maximized. The interpretation of the PCs, however, may correspond to some subjectively meaningful constructs, but this is not guaranteed in the model assumption.

In contrast, FA is a generative model with the built-in assumption that a number of latent factors led to the observed features. The factors are usually derived from EM algorithms assuming the distribution of the data is generated according to multi-variate Gaussians.

Consequences

FA reconstructs and explains all the pairwise covariances with a few factors, while PCA cannot do it successfully. This is because PCA extracts eigenvectors of the data distribution, while FA seeks to find latent factors that maximizes the covariances explained. Note that it doesn’t make much sense to treat the factors from FA as a “direction” in the feature space as in PCA because it’s not a transformation of the feature space.

A very useful illustration is given in ttnphns’ stackexchange post, showing this difference:

The error of reconstruction using either PC1 or F1 will have different shape in the feature space. The error resulting from FA reconstruction are uncorrelated in the feature space, while that from PCA reconstruction is.

Applications

When to use PCA vs. FA?

Ideally, if the goal is find latent explainatory variables, then FA’s generative model assumption is better suited. If the goal is to perform dimensionality reduction, such as when trying to conduct regression model with highly correlated features, PCA would be preferred.

So why would so many papers use PCA instead of FA, and interpret principal components to represent some latent factors?

The interpretation here is theoretically not sound. But practically this is ok, since as the number of features \(n\) increases, the results of PCA approaches FA. See amoeba’s great simulations on stackexchange, as well as ttnphns’s simulations.

Why is this the case, if the model formulation and computations are so different? Referencing amoeba –

From model formulations, PCA finds \(\mathbf{W}\) to best approximate the sample covariance matrix such that \(\mathbf{C}\approx\mathbf{W}\mathbf{W}^T\), while FA finds \(\mathbf{W}\) to best approximate the off-diagonal entries of \(\mathbf{C}\), i.e. \(offdiag(\mathbf{C})\approx\mathbf{W}\mathbf{W}^T\) (remember that FA tries to capture the pairwise correlation between features). The diagonal elements of \(\mathbf{C}\) in FA is taken care of by \(\mathbf{\Psi}\).

This means:

1. If the diagonals of \(\mathbf{C}\) are small (i.e. all features have low noise), meaning that the off-diagonal elements dominate \(\mathbf{C}\), then FA approaches PCA.
2. If \(n\) is very big, then the size of \(\mathbf{C}\) is also very big, and therefore the contribution of the diagonal elements is small compared to that of the off-diagonal elements, then once again PCA results approach FA. A good way to think about this is in terms of the residual reconstruction error picture – when \(n\rightarrow\infty\), the residual error from PC-reconstruction becomes more isotropic, approaching that of FA.

When is \(n\) large enough for PCA to approximate FA?

When the ratio \(n/k\), where \(k\) is the expected number of latent factors, is big. Usually a ratio of 10 is a good threshold from simulation results. This also explains my past observations in neural data – where the number of features is ~100 (number of neurons), and latent factors is ~10 (cursor/actuator position/velocity).

The other, more practical reason is simply that PCA is way more easier to compute!

If PCA approaches FA under large n, why use FA at all?

Beyond better model assumptions for the question investigation, FA formulations enables easier interpretation of shared covariances and its relationship with pairwise correlations. This was the key insight in Umakantha2021, for example.

Conclusions

1. PCA and FA differ in model assumptions, notably, FA assumes the data is generated by some underyling latent factors.
2. PCA seems to approximate the data distribution while minimizing the diagonal reconstruction errors of the covariance matrix, while FA seeks to minimize the offdiagonal reconstruction errors of the covariance matrix.
3. PCA approaches FA results when the number of features is big compared to the assumed number of latent factors.

Still not great at matrix math – why are they so much harder than trig identities…

Great reference on matrix identities and derivations, saved a copy here.

Bridging neuronal correlations and dimensionality reduction

Pairwise correlations between individual neurons, and dimensionality reduction based methods to characterize population statistics are widely used to measure how neural populations covary. This paper establishes mathematical relationships between the two approaches and demonstrate that summarizing population-wide covariability using any single activity statistic is insufficient.

The graphical abstract and highlights on the publication are actually very informative after reading through some of the paper:

As is typical Byron Yu/Aaron Batista fashion, this paper presents a clever application of dimensonality reduction (specifically factor analysis).

Neuroscience literature often presents pairwise statistics to characterize neural populations (i.e. average spike-count correlations before and after learning BMI). They first propose that that this measure \(r_{sc}mean\) needs to be complemented by the pairwise metric standard-deviation \(r_{sc}SD\), then connect how the changes in this pair of pairwise metrics relate to population-level metrics obtained through dimensionality reduction.

The next three figures illustrate the population-level metrics, and their relationship with pairwise metrics. The central idea is that the population activity can have different degree of covariation, which can be decomposed into shared variation along a number of latent fluctuations.

1. Loading similarity: How correlated population activities are.
2. Percent-shared variance: How much each neuron’s fluctuatons is captured by the latent co-fluctuation.
3. Dimensionality: The number of “co-fluctations” needed to capture the variance in the population activities (similar to number of PCs in PCA).

If all these sounds like factor analysis (FA), that’s because it’s a different way of interpreting F.A. The crux of the paper below:

The field of DSP is pretty broad, but I found knowing/remembering the following basic concepts are both useful in practice, and in interviews (giving or receiving). Understanding the concepts below can also make debugging unexpected results much easier, and I’ve had to come back to these concepts many times.

FIR vs. IIR filters

1. FIR filters are easy to implement, always causal.
2. IIR filters are more concise to implement, but it requires feedback. Can implement higher order IIR filters with biquad structures (SOS-implementations) for stability (not needed for FIR).
3. FIR filters are always linear phase.
4. IIR filters can try to be linear phase within the passband.

Phase Delay

1. Linear phase is when the phase-shift introduced to different frequencies are linearly increasing.
2. This means higher-frequency signals are delayed more in phase.
3. The result is that all frequencies are delayed the same in time, despite differently in phase.
4. Intuitively, linear phase means the filtered signal will have similar shape as before.

Spectrum Leakage

1. This phenomenon stems from the assumption of DFT, that the input signal is ONE PERIOD of a PERIODIC SIGNAL.
2. If the part of the signal that is windowed is not an integer multiple of the periodic signal, then the resulting frequency spectrum may not have frequency bins corresponding exactly to the frequency of interest – the resulting DFT is not sharp, and
3. The frequency of interest is “spread” out into the surrounding frequency bins. producing a “leakage”.
4. This can be solved with “zero-padding”, adding zeros to the end of the time-domain signal. This approximates the effect of taking the CTFT of a windowed periodic signal.
5. The result is that the DFT of this zero-padded signal looks like an interpolation of the previously “spread-out” DFT of the non- zero-padded signal. For signal with a single tone, this would recover the correct peak frequency.
6. Zero-padding does not improve frequency resolution (interpolation doesn’t increase resolution). To improve resolution we need longer duration recording of the signal.

FFT^2 vs. PSD of a signal

1. PSD usually applies to a stochastic process (usually stationary). For non-stationary processes such as speech, STFT should be used.
2. Wiener-Khinchin Theorem: For stationary stochastic process, PSD is defined as the Fourier Transform of the Autocorrelation Sequence of the signal. From this we get the amount of power per frequency bin.
3. PSD can be estimated by taking the magnitude squared of the FT of the signal – this is called the Periodogram.
   • This is not a consistent estimator as it does not tend to a limit with increasing sample size, as the individual values are exponentially distributed.
4. An alternative is to get a truncated version of the auto covariance signal, then take the Fourier Transform.
   • This leads to spectral window of some width, has lower sampling variability and with minor assumptions IS a consistent estimator.
5. The key weakness of the periodogram is that it takes only one “realization” of a stochastic process and therefore has high variability..
   • The PSD can be thought of as a random variable – you need to average over many outcomes to get a decent estimate
   • In fact, another definiton of PSD is “an average of the magnitude squared of the Fourier Transform”.
   • Very CHEAP computationally, but has high variance.
6. Consequently, averaging multiple peridograms can approach the PSD.
7. The unit of PSD is /Hz. Integrating PSD over a delta of frequency bin gives the energy (Watts).
8. For a mean-zero signal, integral of the entire PSD is equal to the variance.
9. Key Duality: a quadratic quantity in the frequency domain (energy spectral density in determinstic case, power spectral density in the stochastic case) corresponds to a correlation (which is essentially a convolution) in the time domain.
10. Multi-taper approach Is a fancy way of averaging periodograms. It averages a pre-determined number of periodograms obtained by different window (taper) on the same signal. The windows selected have two key properties:
    • The windows are orthogonal, this means that the periodgrams are uncorrelated, so averaging multiple peridograms give an estimate with lower variance than using just a single taper.
    • The windows have the best possible concentration in the frequency domain for a fixed signal length to minimize spectral leakage.
    • Probably the best estimator for stationary time-series that’s not super long..
11. Informative resource with a good discussion on why so many PSD calculations: 1

Savitzky-Golay filter

I actually haven’t encountered this in grad school, probably because I dealt mostly with spikes, and didn’t need the smoothing abilities that SGF is especially suited for. Everyone in my job seems to love it for some handwavy reason so I wanted to demystify it. A good overall discussion of the pros/cons beyond the basic formulation is on stackoverflow. Some highlights:

1. Let’s get it straight, SGF is not magical, adaptive or anything. It’s an FIR filter designed with local polynomial approximation.
2. If the noise spectrum significantly overlaps with the signal spectrum, a more careful approach is required, and brute-force attenuation will not work well because either you leave too much noise (by choosing the cut-off frequency too high) or you distort the desired signal too much. In this case Savitzky-Golay (S-G) filters may be a good choice.
3. SGF tutorial:
   • Can be thought of a FIR low-pass filter, with flat passband, and moderate attenutation in the stop band.
   • Good for preserving peak shapes and height, bad for rejecting noise.
   • Use when you want to smooth, but the noise and signal share similar frequency.
4. SGF with smaller window length means less attenuation in higher frequencies, this means it distorts the peaks less, but noise that’s slightly out of the band are not filtered as sharply.
5. Longer window attenuates more, but keeps the amplitude constant for a basic sinusoid.
6. Examples/Tests:
   • Clean signal of 1Hz, corrupt with 10Hz, and 40Hz (yes the noise are out of band). Len-31 sgf would perform better than len-101 because it distorts the peaks less, and the resulting waveform is almost identical to the base 1Hz waveform.
   • Clean signal of 1Hz, corrupt with 1.2Hz and 40Hz. Len-31 sgf results in a smoother version of the original signal. Len-101 sgf results in a 1Hz signal with smaller amplitude. In this case, Len-101 correctly filtered out the high frequency components better.
7. In practice, I actually found SGF to be hard to use/tune. Much better to do actual adaptive filtering (e.g. H-infinity, LMS) if a noise measurement is available.

Utilizing ergodicity to increas SNR

• In diffusion correlation spectroscopy, for example, SNR is proportionally to photon rate (more signal per time), and integration time (for more accurate auto-correlation calculation).
• However, more than one measurement can be taken at a time, increasing the number of measurements spatially can then achieve similar SNR increase as a greater photon rates and/or integration time.
• This is based on the assumption of ergodicity – i.e. a random process averaged over time/space has the same mean and variance.

Time Series ARIMA models and Signal Processing relations

1. PSU stats510 is a great reference for the basics.
2. Moving Average (MA) are like FIR filters
3. Autogressive (AR) models are like IIR filters.
4. Every autoregressive-integrated-moving-average (ARIMA) model can be converted to an infinte order MA model – similar to how IIR filters can be approximated by FIR filters!
5. When decomposing (trend + seasonal + random) additive models, trend is extracted by sliding window centered moving averages (similar to low-pass filtering), with a window length equal to the seasonal span.
6. Smoothing: LOWESS/LOESS are equivalent to Savitzky-Golay – i.e. fitting regressions or polynomials locally to each point, may include weighting function applied to different points.
7. We shouldn’t blindly apply exponential smoothing because the underlying proces smight not be well modeled by an ARIMA(0,1,1). The reason is that Exponential Moving Average (EMA) is equivalent to a first-order moving average (MA1) model.
8. Diagnostics:
   • AR models should show decaying autocorrelation function (ACF) and cutoff in partial autocorrelation function (PACF).
   • MA models should show cutoff ACF, and decaying PACF.
   • ACF and PACF both showing spike-cutoff patterns suggests ARIMA model.
   • Seasonal trends show periodic cutoff ACF or PACF
9. How to fit ARIMA model to linear model residuals:
   • Cochrane-Orcutt (example) does pre-whitening, then apply OLS to get the beta coefficients and SE. R-squared after this procedure is ususually less than that of LS
   • ARIMAX: Fitting regression with ARIMA error structure, can be done with Cochrane-Orcutt, but better with maximum-likelihood estimation to joint estimate both the regression model and error ARIMA model.
   • Can treat this as a state-space model – the ARIMA error describes the state transition, the exogeneous regressors describe the observation model.
   • Some connection to Kalman filtering after some manipulations.

Yule-Walker…because I can never remember this name..

1. Yule-Walker equations is used to fit AR model of certain orders.
2. Order structure is determined by maximum-likelihood or AIC of the fit to the residuals.
3. Wiener-Hopf equation is a generalization of the Yule-Walker equations.

DSP-implementation gotchas:

1. SOS/biquad implementation are better than transfer function implementations in practice due to robustness in overflow and quantization error. For example, see scipy issue.
2. When implementing cascade of filters in DSP, it’s important to think about and set the initial conditions for the 2nd stages and on. These filter stages should have initial condition set to the step response steady-state of the previous filter, corresponding to that state’s initial state, and so on.

My newest hobby is high-altitude mountaineering. There’s so much different advices out there about how to improve endurance and speed, to go faster for longer. Information from runners and climbers and cyclists can be very different.

I got nerdy and dug into the physiology and evaluated the main training methods:

• Long-duration low-intensity (LD)
• Interval/tempo-runs/maximal-steady-state (Interval)
• High intensity interval training (HIIT)

To find which one or combination is the most optimal training solution for climbing big mountains, along with other training techniques.

Here is my summary. Interestingly, I found the recommended polarized training combination of LD and HIIT to be the same as the one I experienced during college crew, and also similar to Nimsdai’s training (he doesn’t do much HIIT though).

If you have time, go read Training for the new alpinim book, it’s legit and it passes my personal physiology check.

Now I can get ahead with my training without constantly wondering if I’m doing the most optimal things (why don’t you get a coach, d00d?!)

Challenge Point: A framework for conceptualizing the effects of various practice conditions in motor learning

Challenge point framework is a generalization of the 85% optimal learning rule result. Perhaps it’s better to call the 85% optimal learning rule as a prediction within the challenge point framework (which came before).

Essentials

The Challenge Point Framework (CPF) provides a conceptual framework for factors influencing motor skill learning (unclear if it applies to cognitive learning, but some empirical observations in education and language learning seems to suggest so).

The main interacting factors in this framework are:

• Skill level of the learner regarding a specific task
• Task difficulty
• Practice environment

The CPF suggests that as one’s skill increase in a task, learning is optimized when task difficulty is increased as well. This relationship is explained by higher ability to utilize additional information for learning when task skill increases, and additional information improves learning. In contrast, extra information presented during to someone with a low skill level, and thus low ability to utilize information, impedes the learning process by overwhelming the cognitive resources available during learning.

A key idea is that increasing task difficulty is associated with increasing information available to the learner for the following reasons:

1. Model someone being highly skilled in a motor task with the expected success of his movement plan in the task being very high. In this case, a negative result would yield more information about the learner’s internal model. In contrast, a positive result does not provide much useful information.
2. When task difficulty is low, he would expect success, therefore learning is minimal.
3. When task difficulty is high, likelihood for negative result is higher, therefore the potential information available to the learner is higher. More potential information implies more learning is possible.

A related way to see it is that “practice leads to redundancy, less uncertainty, and, hence, to reduced information”. The more that practice leads to better expectations, the less information there will be to process.

Therefore in this framework, factors that contribute to motor learning can be easily evaluated to predict its effects on skill performance and learning. Factors influencing learning include:

1. Task difficulty: note this can be divided into the inherent or nominal difficulty, and functional difficulty. A nominally difficult task can be made to have less functional difficult task by introducing helpful feedback, for example.
2. Practice schedule (changes the functional difficulty): blocked, random, randomized block. Random practice schedule increases the functional difficulty wrt blocked practice schedule due to contextual interference.
3. Feedback (also known as knowlege of result - KR) and feedback schedule:
   • More frequent feedback lowers functional difficulty
   • Random feedback schedule increases functional difficulty, compared to blocked schedule.

This framework also predict optimal challenge point, as a function of task difficulty and skill level, during which learning (or utilizable potential information availability) is maximized.

Details

Definitions

Nominal task difficulty: The difficulty of a particular task within the constraints of an experimental protocol. The nomianl difficulty of a task is considered to reflect a constant amount of task difficulty, regardless of who is performing the task and under what conditions it is being performed. This makes the most sense in comparison with other skills, for example, kicking a ball 50 meters has more nominal difficulty than kicking it 1m, and less than kicking it 100 meters.

Functional task difficulty: How challenging the task is relative to the skill level of the individual performing the task and to the conditions under which it is being performed. Ex: kicking a ball 50 meters has the same nominal difficulty to amateur and pro, but different functional difficulty (i.e. success rate).

Practically, nominal task difficulty is probably not important to think about.

Assumptions

Learning is a problem-solving process in which the goal of an action represents the problem to be solved and the evolution of a movement configuration represents the performer’s attempt to solve the problem.

Source of information available during and after each attempt is remembered and form the basis for learning, resulting in improvement skill – this is practice.

Two sources of information are criticle for learning: the action plan (known to a priori to the learner), and feedback (obtained during or after).

Optimal challenge point

In CPF, learning is directly related to the information available and interpretable in a performance instance, which, in turn is tied to the functional difficulty of the task. The central thesis is then:

Information represents a challenge to the performer and that when information is present, there is potential to learn from it

Subsequent corollaries are:

1. Learning cannot occur in the absence of information
2. Learning will be impeded in the presence of too much information (too much challenge, cognitive overload).
3. Learning achievement depends on an optimal amount of information, which differs as a function of the skill level of the individaul.

Therefore, the factors contributing to functional task difficulty interact to dictate the optimal amount of interpretable information, and thus the potential for learning.

Corollary 2 derives from the observation that if information is to result in learning, it must be interpretable. The total amount of information one can interpret is goverend by one’s information-processing capabilities, which changes with practice.

As skill improves, the expectation for performance becomes more challenging. So to generate a challenge for learning, one must obtain increased information, which can arise only from an increase in the functional task difficulty. Luckily, both information-processing capability and skill level increases with practice.

Predictions of CPF

1. Practice variables that influence action planning information via contextual interference (most often random practice schedule is proxy for contextual interference):
   • For tasks with differing levels of nominal difficulty, the advantage of random practice (vs. blocked practice) for learning will be largest for tasks of lowest nominal difficulty and smallest for tasks of highest nominal difficulty.
   • For individuals with differing skill levels, low levels of CI will be better for beginning skill levels and higher levels of CI will be better for more highly skilled individuals (via increasing functional difficulty).
   • Modeled information (i.e. examples and prior demos) decrease functional difficulty.
2. Practice variables that influence feedback information (knowledge of result, among other things):
   • For tasks of high nominal difficulty, more frequent or immediate presentation of KR, or both, will yield the largest learning effect. For tasks of low nominal difficulty, less frequent or immediate presentation of KR, or both, will yield the largest learning effect
   • For tasks about which multiple sources of augmented information can be provided, the schedule of presenting the information will influence learning. For tasks of low nominal difficulty, a random schedule of augmented feedback presentation will facilitate learning as compared with a blocked presentation. For tasks high in nominal difficulty, a blocked presentation will produce better learning than a random schedule.

How to apply?

1. Athletic skills is perhaps the obvious example: boxers practice individual punches first (blocked practice schedule, frequent feedback, easy), before mixing it in combinations and sparring.(random practice schedule, summary/infrequent feedback, difficult).
2. Tutorials: Introduce concept one at a time (less information and less difficulty)

The Eighty Five Percent Rule for optimal learning

A practice schedule or learning plan can be very important in skills and knowledge acquisition, thus the saying “perfect practice makes perfect”. I first heard about this work on Andrew Huberman’s podcast on goal setting. The results here are significant, offering insights into both training ML algorithms, as well as biological learners. Furthermore, the analysis techniques are elegant, definitely brushed off some rust here!

Summary

1. Examine the role of the difficulty of training on the rate of learning.
2. Theoretical result derived for learning algorithms relying on some form of gradient descent, in the context of binary classification.
   • Note that gradient descent here is defined as where “parameters of the model are adjusted based on feedback in such a way as to reduce the average error rate over time”. This is pretty general, and both reinforcement learning, stochastic gradient descent, and LMS filtering can be seen as special cases.
3. Results show under Gaussian noise distributions, the optimal error rate for training is around 15.87%, or conversely, the optimal training accuracy is about 85%.
   • The noise distribution profile is assumed to be fixed, i.e. the noise distribution won’t change from Gaussian to Poisson.
   • The 15.87% is derived from the value of normal CDF with value of -1.
   • Under different fixed noise distributions, this optimal value can change.
4. Training according to fixed error rate yields exponentially faster improvement in precision (proportional to accuracy), compared to fixed difficulty. \(O(\sqrt(t))\) vs. \(O(\sqrt(log(t)))\).
5. Theoretical results validated in simulations for perceptrons, 2-layer NN on MNIST dataset, and Law and Gold model of perceptual learning (neurons in MT area making decision about the moving direction of dots with different coherence level, using reinforcement learning rules).

Some background

The problem of optimal error rate pops up in many domains:

• Curriculum learning, or self-paced learning in ML.
• Level design in video games
• Teaching curriculum in education

In education and game design, empirically we know that people are more engaged when the tasks being presented aren’t too easy, and just slightly more difficult. Some call this the optimal conditions for “flow state”.

Problem formulation

The problem formulation is fairly straight-forward, as the case of binary classification and Gaussian noise.

1. Agent make decision, represented by a decision variable \(h\), computed as \(h=\Phi(\mathbf{x}, \phi)\), where \(\mathbf{x}\) is the stimulus, and \(\phi\) are the parameters of whatever learning algorithm.
2. The decision variable \(h\) is a noisy representation of the true label \(\Delta\): \(h = \Delta + n\), where \(n \approx N(0, \sigma)\).
3. If the decision boundary is set at \(h=0\) (see Figure 1A), such that chose A when \(h<0\), B when \(h>0\) and randomly otherwise, then the decision noise leads to error rate of: \[ER = \int_{-\infty}^{0} p(h|\Delta,\sigma)dh=F(-\Delta/\sigma)=F(-\beta\Delta)\].
   • p() is Gaussian distribution
   • F() is Gaussian CDF
   • \(\beta\) is precision, and essentially measures how “peaky” the decision variable distribution is. This can be thought of as the (inverse) accuracy or “skill” of the agent.
   • So, the error decreases with both agent skill (\(\beta\)) and ease of problem (\(\Delta\)).
4. Learning is essentially an optimization problem, to change \(\phi\) in order to minimize \(ER\). This can be formulated as a general gradient descent problem: \[\frac{d\phi}{dt}=-\eta\nabla_\phi ER\].
5. This gradient can be written as \(\nabla_\phi ER = \frac{dER}{d\beta}\nabla_\phi \beta\). And we want to find the optimal difficulty \(\Delta^*\) that maximizes \(\frac{dER}{d\beta}\).
6. \(\Delta^*\) turns out to be \(\frac{1}{\beta}\), which gives optimal error rate \(ER^*\approx 0.1587\).
   • This is nice, the difficulty level should be proportional to the skill level.

Simulations

Validation of this theory boils down to the following elements:

• How to quantify problem/stimulus difficulty \(\Delta\)?
• How to select problem with the desired difficulty?
• How to adjust target difficulty level to maintain the desired error rate?
• How to measure error rate \(ER\)?
• How to measure skill level?

1. Application to perceptron:
   • A fully trained teacher perceptron network’s weights \(\mathbf{e}\) are used to calculate the difficulty. The difficulty of a sample is equal to its distance from the decision boundary (higher is less difficult).
   • Skill level of the network is \(\cot{\theta}\), where \(\theta\) is the angle between the learner perceptron’s weight vector and the teacher perceptron’s weight vector.
   • Error rate is approximately Gaussian and can be determined from the weight vectors of the teacher and learner perceptrons, and the sample vectors.
2. Application to two-layer NN:
   • Trained teacher network. The absolute value of the teacher network’s sigmoid output is the difficulty of a stimulus.
   • Error rate is the accuracy over the past 50 trials (not batch training).
   • Skill level is the final performance over the entire MNIST dataset.
   • Difficulty level is updated with value proportional to the current and target accuracy level.
3. Appliation to Law and Gold model:
   • Simulated update rule of 7200 MT neurons according to the orignal reinforcement model.
   • Coherence adjusted to hit target accuracy level: implicitly measure difficulty level
   • Accuracy/error rate is from past running average
   • Final skill level is from applying ensemble on different coherence level stimulus (disabling learning) and fitting logistic regression.

Implications

1. Optimal rate is dependent on task (binary vs. multi-class), and noise distribution.
2. Batch learning makes things more tricky – depending on agent learning rate.
3. Multi-class may require finer grained evaluation of difficulty and problem preseentation (i.e. misclassifying 1v2, or 2v3).
4. Not all models follow this framework, e.g. Bayesian learner with perfect memory does not care about example presentation order.
5. Can be a good model for optimal use of attention for learning – suppose exerting attention changes the precision \(\beta\), then the benefits of exerting attention is maximized during optimal error rate.

Continuing on my quest to have the best unifying intuition about linear algebra, I came across the excellent series Essence of Linear Algebra on YouTube by 3Blue1Brown.

This series really expanded on the intuition behind the fundamental concepts of Linear Algebra by illustrating them geometrically. I have vaguely arrived at the same sort of intuition through thinking about them before, but never this explicitly. My notes are here.

Chapter 1: Vectors, what even are they

Vectors can be visualized geometrically as arrows in 1-D, 2-D, 3-D, …, n-D coordinate system, and can also be represented as a list of numbers (where the numbers represent the coordinate values).

The geometric interpretation here is important to build interpretation and can later be gneralized to more abstract vector spaces.

Chapter 2: Linear combinations, span, and basis vectors

Vectors (arrows, and list of numbers) can form linear combinations, which can involve multiplication by scalars and addition of vectors. Geometrically, multiplication by scalar is equivlaent to scaling the length of a vector by that factor. Vector addition means putting vectors tail to head and find the resulting vector.

Any vectors in 2D space, for example, can be described by linear combinations of a set of basis vectors.

In other words, 2D space are spanned by a set of basis vectors. Usually, the basis vectors are chose to be \([1,0]^T\) and \([0,1]^T\) in 2-D, representing the unit \(\hat{i}\) and \(\hat{j}\) vectors.

As a corollary, if a 3-by-3 matrix \(A\) has linearly-dependent columns, that means its columns does not span the entire 3D-space (spans a plane or a line instead).

Chapter 3: Linear transformations and matrices

Multiplication of a 2-by-1 vector \(v\) by an 2-by-2 matrix \(A\) to yield a new 2-by-1 vector \(u\): \(Au=v\) can be thought of as a linear transformation. In fact, this multiplication can be thought of as transforming the original 2-D coordinate system into a new one, with the caveat the grid lines still have to remain parallel after the transformation (think about a grid getting sheared or rotated).

Specifically, assume the original vector \(v\) is written with basis vectors \(\hat{i}\) and \(\hat{j}\), the columns of \(A\) can be thought of where \(\hat{i}\) and \(\hat{j}\) land in the transformed coordinate system.

Therefore, the matrix-vector multiplication then has the geometric meaning of representing the original vector \(v\) as linear combination of the original basis vectors \(\hat{i}\) and \(\hat{j}\), finding where they map to in the transformed space (indicated by matrix \(A\)), and then yielding \(u\) as the same linear combination of the transformed basis vectors.

This is a very powerful idea – the specific operation of matrix-vector multiplication makes clear sense under this context.

Chapter 4: Matrix multiplication as compositions and Chapter 5: Three-dimensional linear transformations

If a matrix represents a transformation of the coordinate system (e.g. shear, rotation), then multiplication of matrices represent sequences of transformations. For example \(AB\) can represent first shear the coordinate system (\(B\)) then rotate the resulting coordinate system (\(A\)).

This also makes it obvious why matrix multiplication is NOT commutative. Shearing a rotated coordinate system can have different end result as rotating a sheared coordinate system.

Inverse of a matrix \(A\) then represents performing the reverse coordinate system transformation, such that \(A^{-1}A=AA^{-1}\) represents net-zero transformation of the original coordinate system, which is exactly represented by the identity matrix.

Chapter 6: The determinant

This is a really cool idea. In many statistics formulas, there will be a condition that reads like “assuming \(A\) is positive-definite, we multiply by \(A^{-1}\)”. Positive-definite relates to positive determinants. This gave me the sense that determinant represents a matrix analog of real number’s magnitude. But then what does a negative determinant mean?

In the 2D case, if a matrix represents a transformation of the coordinate system, the determinant then represents the area in the transformed coordinate system of a unit area in the original system. Imagine a unit square being stretched, what is the area of the resulting shape – that is the value of the determinant.

Negative determinant would mean a change in the orientation of the resulting shape. Imagine a linear transformation as performing operations to a piece of paper (parallel lines on the paper are preserved through the operations). Matrix with determinant of -1 would correspond to operations that involve flipping the paper. \(\hat{i}\) is originally 90-degrees clockwise from \(\hat{j}\), after flipping the paper (x-y plane), \(\hat{i}\) is now 90-degrees counter clockwise from \(\hat{j}\).

In 3D, determinant then measures the scaling a volume, and negative determinant represent transformations that does not preserve the handed-ness of the basis vectors (i.e. right-hand rule).

If negative determinant represent flipping a 2D paper, then 0 determinant would mean a unit-area becoming zero. Similarly, in 3D, 0 determinant would mean a unit-volume becoming zero. What shape has 0 volume? A plane, a line, and a point. What shape has 0 area? A line and a point.

So if \(det(A)=0\), then we know \(A\) transforms maps vectors into a lower-dimensional space! And that is why positive-definiteness is important, it means a transformation perserves the dimension of the data!

From this intuition, the computation of determinant also makes a bit more sense (at least in the 2D case).

Chapter 7: Inverse matrices, column space and null space

This chapter combines the geometric intuition from before and solving systems of linear equations to explain inverse matrices, column space, and null space.

Inverse matrices

Solving system of linear equations in the form of \(Ax=v\) (wlg, A=3-by-3, x and v are 3-by-1 vectors) can be thought of as what vector \(x\) in 3-D space, after transformation represented by \(A\), become the vector \(v\)?

In this nominal case where \(\|det(A)\|>0\), there exists an inverse \(A^{-1}\) that represents the inverse transformation represented by \(A\), and thus \(x\) can be solved by multiplying \(A^{-1}\) on both sides of the equation.

Intuitively this makes sense – to get the vector pre-transformation, we simply reverse the transformation.

Now suppose \(\|det(A)\|=0\), this means \(A\) maps a 3-D vector onto a lower-dimensional space, which can be a plane, a line, or even a point. In this case, no inverse \(A^{-1}\) exists, because how can you transform these lower-dimensional constructs into 3D space? (Note that in most textbooks, the justification of \(A^{-1}\) exists only when \(det(A)\) is not zero is made on the basis of Gauss-Jordan form, which is not intuitive at all).

Column Space and Null Space

So in the nominal case, each vector in 3D is mapped to a different one in 3D space. Therefore the set of all possible \(v\)’s span the entire 3D space. Therefore the 3D space is the column space of the matrix \(A\). The rank of \(A\) in this case is 3, because the column space is 3-dimensional.

The set of vectors \(x\) that after transformation by \(A\) yield the 0-vector are called the null space of the matrix \(A\).

In cases where \(det(A)=0\), the columns of \(A\) must be linearly dependent, this means its column space is not 3-dimensional, and therefore its rank is less than 3 (and therefore is rank-deficient and not full-rank for a 3-by-3 matrix).

If this rank-deficient \(A\) maps \(x\) onto a plane, then its column space has rank 2. Onto a line – rank 1; Onto a point – rank 0. For a 3-by-3 matrix, 3 minus the rank of the column space is the rank or dimension of the null-space.

Geometrically, this means if a transformation compresses a cube into a plane, then an entire line of points are mapped onto the origin of the resulting plane (imagine a vertical compression of a cube, the entire z-axis is mapped onto the origin and is therefore the null space of this transformation). Similarly, if a cube is compressed into a line, then an entire plane of points are mapped onto the origin of the resulting number line.

Left and Right Inverse

Technically, the inverse \(A^{-1}\) normally talked about refers to the left inverse (\(A^{-1}A=I\)). And the full-rank matrices for which left inverse exist perform a one-to-one transformation of vectors (injective) – each unique vector \(x\) is mapped onto at most one \(v\) vector.

For matrices with more columns than rows, the situation is a bit different. Using our intuition from before treating the columns of matrix as mapping of the original basis vectors into a new coordinate system, consider the matrix \([1, 0; 0, 1; 0, -1]\) mapping a 3D vector. This matrix maps the basis vectors \([1, 0, 0]^T\), \([0, 1, 0]^T\) and \([0, 0, 1]^T\) onto an entire plane, respectively. Therefore each transformed vector can have multiple corresponding vectors in the original 3D space (therefore \(A\) is called surjective).

Consequently, if \(A\) is 2-by-3, there exists a 3-by-2 right-inverse matrix \(B\) such that \(AB=I\), but here \(I\) is 2-by-2. Geometrically, this is saying if we transform a 2D vector onto 3-space (\(B\)), we can recover this 2D vector by another transformation (\(A\)). Thus right-inverse deal with transformations involving dimensional changes.

These explanations, in my opinion, are much more intuitive and easy to remember than the rules and diagram taught in all of the linear algebra courses I have ever taken, including 18.06.

Chapter 8: Nonsquare matrices as transformations between dimensions

This is straight forward applying the idea that the columns of a matrix represent mapping of the basis vectors.

Chapter 9: Dot product and duality

This one is pretty interesting. Dot product represents projection. At the same time, we can think of dot product in 2D, \(v \cdot u\) as a matrix-vector multiplication \(v^T u\). Here we can think of the “matrix” \(v^T\) as a transformation of the basis 2D basis vectors \(\^{i}\) and \(\^{j}\) onto vectors on the number line. Therefore dot-product represents a 2D-to-1D transformation.

This is the idea of vector-transformation duality. Each n-dimensional vector’s transpose represents an N-to-1 dimensional linear transformation.

Chapter 10: Cross products

This one is also not too insightful, perhaps because cross product’s definition as a vector was strongly motivated by physics.

Cross-product of two 2D vectors \(a\) and \(b\) yield a third vector \(c\) perpendicular to both (together obeying right-hand rule) with magnitude equal to the area of the parallelogram formed by the \(a\) and \(b\). Thinking back, cross-product formula involves calculating a type of determinant – which makes sense in terms of the area interpretation of the determinant.

Then the triple product \(\|c\cdot(a\times b)\|\) represents the volume of the parallelpiped formed by \(a\), \(b\), and \(c\).

Chapter 11: Cross products in the light of linear transformations

This one basically explains the triple product by interpreting the dot-product operation (\(c\cdot(\cdot)\)) by the cross-product (\(a\times b\)) as finding a 3D-to-1D linear transformation.

Not too useful.

Chapter 12: Change of basis

This also follows from the idea that a matrix represents mapping of the individual vectors of a coordinate system.

The idea is that coordinate systems are entirely arbitrary. We are used to having \([1,0]^T\) and \([0,1]^T\) as our basis vectors, but they can be a different set entirely. Suppose Jennifer has different basis vectors \([2,1]^T\) and \([-1,1]^T\), how do we represent a vector \([x_0,y_0]^T\) in our coordinate system in Jennifer’s coordinate system?

This is done by a change of basis – by multiplying \([x_0,y_0]^T\) by a matrix whose columns are Jennifer’s basis vectors. This is yet another application of matrix-vector product.

Change of basis can also be applied to translate linear transformations. For example, suppose we want to rotate the vector \(u=[x_1,y_1]^T\) in Jennifer’s coordinate system by 90 degrees and want to find out the result in Jennifer’s coordinate system. It may be tedious to figure out what the 90-degree transformation matrix is in Jennifer’s coordinate system, but it is easily found in our system (\([0,-1;1, 0]\)).

So we can achieve this easily by first transforming \(u\) into our coordinate system by multiplying it by the mapping between Jennfier and our coordinate system. Then apply the 90-degree transformation matrix, then apply the inverse transformation to get back the resulting vector in Jennifer’s system.

This is a powerful idea and relates closely to eigenvectors, PCA, and SVD. SVD especially represents a matrix by a series of coordinate transformations (rotation, scaling and rotation).

Chatper 13: Eigenvector and eigenvalues

This is motivated by the problem \(Av=\lambda v\), where \(v\) are the eigenvectors, and \(\lambda\) are the eigenvalues of the matrix \(A\) (nominally, \(A\) is a square matrix, otherwise we use SVD, but that is beside the point).

The eigenvectors are vectors that, after transformation by \(A\), still point at the same directions as before. A unit vectors before after the transformation may have different length while pointing to the same direction, the change in length is described by the eigenvalue. A negative eigenvalue means the eigenvectors have reversed where it points to after the transformation.

The imagery is suppose we have a square piece of paper/mesh, we pull at the top right and bottom left corners to shear it. A line connecting this two corners will still have the same orientation, though have longer length. Thus this line is an eigenvector, and the eigenvalue will be positive.

However, if a matrix represents rotation, then the determinant will be 0, and the eigenvalues will be imaginary. Imaginary eigenvalues means that a rotation is involved in the transformation.

Chapter 14: Abstract vector spaces

This lesson extrapolate vectors, normally thought of as arrows in 1- to 3-D space and corresponding list of numbers, to any construct that obey the axioms of vector space. Essentially the members of a vector space follow the rule of linear combination (or linearity).

An immediate generalization is thinking of functions as infinite-dimensional vectors (we can add scalar multiples of functions together and the result obey the linearity rule). We can further define linear transformations on these functions, similarly to how matrices are defined on geometric vector spaces.

An example of linear transformation on function is derivative.

This insight is pretty cool and really ties a lot of math and physics concepts together (ex. modeling wavefunctions as vectors in quantum mechanics, eigen-functions as analogs of eigen-vectors).

Writing my dissertation I chose to use Latex because it makes everything looks good, I can stay in Vim, type math easily, and don’t have to deal with an actual Word-like processor’s abysmal load speed when I’m writing 100+ pages. At the same time, some things that should be very easy took forever to figure out.

Problem

In addition to the bibliography of the actual dissertation chapters itself, I need to append a list of my own publications in the biography section (last “chapter” of the entire document), formatted like a proper bibliography section. Why biography? So future readers would known which John Smith you are, of course!

This is difficult for several reasons.

The top level dissertation.tex is something like

\documentclass[]{dissertation}
% Package setup, blabla
\begin{document}
\tableofcontents
\listoftables
\listoffigures
\include                 % Separate tex-file and folder for other chapters
\include
% \include for all the chapters
% Now in the end insert a single bibliography for all the chapters
\bibliographystyle{myStyle}                     % uses style defined in myStyle.bst
\addcontentsline{toc}{chapter}{Bibliography}    % Add it as a section in table of content
\bibliography{dissertation_bib_file}            % link to the bib file 
\include
\end{document}

If I were using word, I might just copy and paste some formatted lines to the end of the page and call it a day. But since I am a serious academic and want to do this the right away…it poses a slight struggle. I need to make bibtex format my publications and insert it at the end during the compile process. My requirements:

1) I don’t want the publication list to start with a “Reference” section heading like typical \bibliography{bib_file} commands produce.

2) I want the items in the publication list to be in reverse chronological order, from most recent to least.

3) I want to allow my publication list to be separate from the main bibliography section – an item can appear in both places, but they should have the same numbering.

Approach 1

Created a separate bibtex file mypub.bib, then inserted the following lines in biography.tex:

\nocite{*}                      % needed to show all the items in the bib-file. 
                                % Otherwise only those called with \cite{}
\bibliographystyle{myStyle}     % uses style defined in myStyle.bst
\bibliography{mypub}            % link to second bib file 

I don’t remember the exact behavior, but it either

1) Gives error, pdflatex tells me I can’t call \bibliography in multiple places. Or 2) Insert the entire dissertation’s bibliography after the biography section.

Neither is desirable.

Approach 2

Searching this problem online, you run across people wanting to

1) Have a bibliography section for each chapter 2) Divide biblography into nonoverlapping sets, such as journals, conference proceedings, etc.

Don’t want those. Finally found this SO post How to use multibib in order to insert a second bibliography as a part of an annex?, which other than suggesting using multibib, also mentions biblatex would make everything a lot easier. But that required me to change the other chapters a bit. Also the manual to multibib.

So new approach, in dissertation.tex:

% preamble stuff
\usepackage{multibib}
\newcites{pub}{headingTobeRemoved}  % create a new bib part called 'pub' with heading 'headingTobeRemoved`
\begin{document}
% all the chapter includes
% Now in the end insert a single bibliography for all the chapters
\bibliographystyle{myStyle}                     % uses style defined in myStyle.bst
\addcontentsline{toc}{chapter}{Bibliography}    % Add it as a section in table of content
\bibliography{dissertation_bib_file}            % link to the bib file 
\include
\end{document}

In biography.tex:

Blablabla memememememe
\nocitepub{*}
\bibliographystylepub{myStyle}
\bibliographypub{mypub}

Really important in the second reference section to use \nocitepub, \bibliographystylepub, and \bibliographypub such that it matches the name of the \newcites group.

Also important to run the following,

pdflatex dissertation.tex
bibtex disseration.aux
bibtex pub.aux
pdflatex dissertation.tex
pdflatex dissertation.tex

where dissertation.aux contains the bib-entries to use in the main document’s reference section, and pub.aux contains that for the biography’s publication list.

This got me a list at the end of the biography chapter. But it starts with a big heading, it’s not in reverse chronological order but alphabetical (because myStyle.bst organizes bibs that way), and the numbering is not diea. For example, one of the item in mypub.bib is also in dissertation_bib_file.bib, and their numbering is the same in both places such that in the publication list, I have item ordering like 1, 2, 120, 37, 5…

No good.

Removing Header

In biography.tex, included the following suggest by SO post

Blablabla memememememe
\renewcommand{\chapter}[2]{}
\nocitepub{*}
\bibliographystylepub{myStyle}
\bibliographypub{mypub}

Internally bibliography implements its header as a section or chapter header, so the \renewcommand suppresses it.

Get rid of weird ordering

This took the longest time and I could not find a satisfactory solution. Using

\usepackage[resetlabels]{multibib}

did not help. Nobody seems to even have this problem…so I gave up and just made the items use bullets instead. In biography.tex:

Blablabla memememeem

\renewcommand{\chapter}[2]{}
% ---- next three lines make bullets happen ---
\makeatletter
\renewcommand\@biblabel[1]{\textbullet} % Can put any desired symbol in the braces actually
\makeatother
% -----------------
\nocitepub{*}
\bibliographystylepub{myStyle}
\bibliographypub{mypub}

Reverse chronological order

This one is very tricky, and requires modifying the actual myStyle.bst file. This SO post gives a good idea of how these bst-files work…they really have a weird syntax. Basically, in every bst file, a bunch of functions are defined and used to format individual reference entries from the bibtex entry, then these entries are sorted and inserted into the final file. The function that likely needs to be changed in all bst-files is the PRESORT function.

plainyr-rev.bst provides a working example of ordering reference entries in reverse chronological order. I decided to use jasa.bst, from Journal of American Statistical Association. The following are the changes needed:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
%%%%%%% Extra added functions %%%%%%%%%%%%%%%
% From plainyr_rev.bst
FUNCTION {sort.format.month}
{ 't :=
  t #1 #3 substring$ "Jan" =
  t #1 #3 substring$ "jan" =
  or
  { "12" }
    { t #1 #3 substring$ "Feb" =
      t #1 #3 substring$ "feb" =
      or
      { "11" }
      { t #1 #3 substring$ "Mar" =
        t #1 #3 substring$ "mar" =
        or
        { "10" }
        { t #1 #3 substring$ "Apr" =
          t #1 #3 substring$ "apr" =
          or
          { "09" }
          { t #1 #3 substring$ "May" =
            t #1 #3 substring$ "may" =
            or
            { "08" }
            { t #1 #3 substring$ "Jun" =
              t #1 #3 substring$ "jun" =
              or
              { "07" }
              { t #1 #3 substring$ "Jul" =
                t #1 #3 substring$ "jul" =
                or
                { "06" }
                { t #1 #3 substring$ "Aug" =
                  t #1 #3 substring$ "aug" =
                  or
                  { "05" }
                  { t #1 #3 substring$ "Sep" =
                    t #1 #3 substring$ "sep" =
                    or
                    { "04" }
                    { t #1 #3 substring$ "Oct" =
                      t #1 #3 substring$ "oct" =
                      or
                      { "03" }
                      { t #1 #3 substring$ "Nov" =
                        t #1 #3 substring$ "nov" =
                        or
                        { "02" }
                        { t #1 #3 substring$ "Dec" =
                          t #1 #3 substring$ "dec" =
                          or
                          { "01" }
                          { "13" } % No month specified
                        if$
                        }
                      if$
                      }
                    if$
                    }
                  if$
                  }
                if$
                }
              if$
              }
            if$
            }
          if$
          }
        if$
        }
      if$
      }
    if$
    }
  if$
 
}

% Original jasa's presort function
%FUNCTION {presort}
%{ calc.label
%  label sortify
%  "    "
%  *
%  type$ "book" =
%  type$ "inbook" =
%  or
%    'author.editor.sort
%    { type$ "proceedings" =
%        'editor.sort
%        'author.sort
%      if$
%    }
%  if$
%  #1 entry.max$ substring$
%  'sort.label :=
%  sort.label
%  *
%  "    "
%  *
%  title field.or.null
%  sort.format.title
%  *
%  #1 entry.max$ substring$
%  'sort.key$ :=
%}

% New one from plainyr_rev.bst
FUNCTION {presort}
{
  % sort by reverse year
  reverse.year
  "    "
  *
  month field.or.null
  sort.format.month
  *
  " "
  *
  author field.or.null
  sort.format.names
  *
  "    "
  *
  title field.or.null
  sort.format.title
  *

  % cite key for definitive disambiguation
  cite$
  *

  % limit to maximum sort key length
  #1 entry.max$ substring$

  'sort.key$ :=
}

ITERATE {presort}

% Bunch of other stuff
% ...
EXECUTE {initialize.extra.label.stuff}

%ITERATE {forward.pass} % <--- comment out this step to avoid the 
                        %       year numbers in the reverse-chronological
                        %       entry to have letters following the year numbers

REVERSE {reverse.pass}

%FUNCTION {bib.sort.order}
%{ sort.label
%  "    "
%  *
%  year field.or.null sortify
%  *
%  "    "
%  *
%  title field.or.null
%  sort.format.title
%  *
%  #1 entry.max$ substring$
%  'sort.key$ :=
%}

%ITERATE {bib.sort.order}

SORT                    % Now things will sort as desired

Extra: Make my name bold

Might as well make things nicer and make my name bold in all the entries in my publication list. This post has many good approaches. Considering I’m likely only to have to do this once (or very infrequently), I decided to simply alter the mypub.bib file.

Suppose your name is John A. Smith. Depending on the reference style and the specific bibtex entry, this might become something like Smith, J. A., Smith, John A., Smith, John, or Smith, J..

In bibtex, the author line may be something like:

% variation 1
author = {Smith, John and Doe, Jane}
% variation 2
author = {Smith, John A. and Doe, Jane}

Apparently the bst files simply goes through these lines, strsplit based on keyword “and”, and take the last name and first name field and contatenate them together. And if only initial is needed, take the first letter of the first name. So, we can simply make the correct fields bold:

% variation 1
author = { {\bf Smith}, {\bf J}{\bf ohn} and Doe, Jane}
% variation 2
author = { {\bf Smith}, {\bf J}{\bf ohn} {\bf A.} and Doe, Jane}

Note that the first name’s first letter and last letters are bolded separately for correct formatting.

Took way too long!

There are some important signal processing points I keep having to re-derive, is rarely mentioned in the textbooks, and buried deep in the math.

What is the physical significance of negative frequencies?

FFT of real signals usually have both positive and negative frequencies in their spectrum. In feedback analysis, we simply ignore the negative frequencies and look at the positive part.

A good illustration of what is actually happening is below:

See also this stackexchange

The spiral can spin counter-clockwise or clock-wise, corresponding to positive or negative frequency. From the formula of Fourier Transform \(F(\omega)=\int_{-\infty}^{\infty} f(t)\exp{-j\omega t}dt\), we can see the frequency spectrum of a signal actually correspond to that of the spiral. Therefore both \(cos(\omega t)\) and \(sin(\omega t)\) are the sum of two complex exponentials. This is in fact true for all real, measurable signals.

In contrast, in Hilbert transform, the analytic signal \(x_c(t)=x_r(t)+jHT\{x_r(t)\}\) has single-sided spectrum, which is not physically realizable. However, it allows us to derive the instantaneous amplitude and frequency of the actual time-domain signal \(x_r(t)\).

Why is a linear phase response desirable for a system?

I always get tripped up by the language. I used to see a phase-response that is not flat and think the different frequencies have different phase lag, therefore they are going to combine at the output and the signal is going to be distorted.

The first part of that thought is correct, but the implication is different. 90-degrees phase-lag for a low-frequency signal is much longer in the time-domain as 90-degrees phase-lag for a high-frequency signal. Therefore, if all frequencies need to be delayed the same amount of time, the phase-lag need to be different.

In math, suppose an input signal \(x(t)=sin(\omega t)\) is filtered to output given by \(y(t)=sin(\omega(t-\tau))\), which is a pure delay by \(\tau\). This can then be written as \(y(t)=sin(\omega t-\omega\tau)=sin(\omega t+\phi(\omega))\), where \(\phi(\omega)=-\omega\tau\) is the phase response of the system, and the phase becomes more negative for larger frequencies.

And this is why linear phase response is desirable for a system.

The success of deep neural network techniques have been so great leading to the hype general intelligence can be achieved soon. I had my doubts, mostly based on the amount of data needed compared to examples needed for people to learn, but also on possible biological mechanisms that could implement backpropagation that is central to artificial neural networks. More neuroscience discoverys are needed.

The great Hinton made a big splash with the capsule theory. Marblestone et al., 2016 had many speculations on how backprop could be approximated by various mechanisms.

Some cool recent results:

1. Delahunt 2018: Biological mechanisms for learning, a computational model of olfactory learning in the Manduca sexta Moth, with applications to neural nets. TR interview

   The insect olfactory system […] process olfactory stimuli through a cascade of networks where large dimension shifts occur from stage to stage and where sparsity and randomoness play a critical role in coding.

   Notably, a transition from encoding of stimulus from a low-dimensional parameter space to one in a high-dimensional parameter space occur, not too common in ANN architectures. Reminds me of the kernel transformations.

   Learning is partly enabled by a neuromodulatory reward mechnaism of octopamine stimulation of the antennal lobe, whose increased activity induces rewiring of the mushroom body through Hebbian plasticity. Enforced sparsity in the MB focuses Hebbian growth on neurons that are the most important for the representation of the learned odor.

   Potential augment to backprop at least. Also, octopamine opens new transmitting channels for wiring expanding the solution space.

2. Akrami 2018: PPC represents sensory history and mediates its effects on behavior. Shows PPC’s role in the representation and ues of prior stimulus information. Cool experiments showing Bayesian aspect of the brain. As much as I dislike Bayesian techniques..

3. Nikbakht 2018 Supralinear and supramodal integration of visual and tactile signals in rats: psychophysics and neuronal mechanisms.

   . Rats combine vision and touch to distinguish two grating orientation categories. . Performance with vision and touch together reveals synergy between the two channels. . PPC neuronal responses are invariant to modality. . PPC neurons carry information about object orientation and the rat’s categorization.

Linear model is a crazy big subject, dividing into:

• LM (linear models) – this includes regressions by ordinary least squares (OLS), as well as all analysis of variance methods (ANOVA, ANCOVA, MANOVA). Assumes normal distribution of the dependent variable.

• GLM (generalized linear models) – linear predictor and dependent variable related via link functions (poisson, logistic regressions fall into this category).

ANOVA and friends (and their GLM analogs) in GLM and LM are achieved through the introduction of indicator variables representing “factor levels”.

• GLMM (generalized linear mixed models) – Extension of GLMs to allow response variables from different distributions. Mixed refers to both fixed and random effects.

A book that seems to have reasonable treatments on the connections is ANOVA and ANCOVA: A GLM approach.

MANOVA, repeated measures, and GLMM

Repeated measures is when the same set of subjects, divided into different treatment groups, are measured over time. It would be silly to treat all of the measurements as independent. Advantage is there is less variance bebetween measurements taken on the same subject. Consequently, a repeated measures design allow for same statistical power with less subjects (compared to another design where N different subjects are measured at the different time points and treating all these measurements as independent).

This can be achieved through:

1. MANOVA approach - The measurements of all subjects at a given time is a length-n vector and becomes the dependent variable of our MANOVA.

2. GLMM - controls for non-independence among the repeated observations for each individual by adding one or more random effects for individuals to the model.

Good explanation

Variance, Deviance, Sum of Squares (SS), Clustering, and PCA

In LM and ANOVA-based methods, we try to divide the total sum of squares (measuring the response deviation of all data points from the grand mean) into components that can be explained by the predictor variables. A good mental picture to have is:

.

Don’t mind that it is in 2D, it actually illustrates the generalization of ANOVA into MANOVA. In ANOVA, response values are distributed along a line, in MANOVA, response values are distributed in n-dimensional space. As we see here, the within-group sum of squares (SSW) is the sum of squared distances from individual points to their group centroid. The among-group sum of squares (SSA) is the sum of squared distances from group centroids to the overall centroid. In ANOVA methods, a predictor’s effect is significant if the F-test statistic, proportional to the ratio of SSA and SSW hits the critical value.

The analogous method is the analysis of deviance in GLM methods, where we are comparing likelihood ratios instead of SS ratios. Still a bitch though.

This framework of comparing dissimilarity or distance is very useful, especially in constructing randomization-based permutation tests. The excellent paper by Anderson 2001 describes how to use this framework to derive a permutation-based non-parametric MANOVA test. This was implemented in MATLAB in the Fathom toolbox.

A key insight is as shown in the following picture

The sum of squared distances from individual points to their centroid is equal to the sum of squared distances divided by the number of points. Why is this important? Anderson explains:

In the case of an analysis based on Euclidean distances, the average for each variable across the observations within a group constitutes the measure of central location for the group in Euclidean space, called a centroid. For many distance measures, however, the calculation of a central location may be problematic. For example, in the case of the semimetric Bray–Curtis measure, a simple average across replicates does not correspond to the ‘central location’ in multivariate Bray–Curtis space. An appropriate measure of central location on the basis of Bray–Curtis distances cannot be calculated easily directly from the data. This is why additive partitioning (in terms of ‘average’ differences among groups) has not been previously achieved using Bray–Curtis (or other semimetric) distances. However, the relationship shown in Fig. 2 can be applied to achieve the partitioning directly from interpoint distances.

Brilliant! Now we can use any metric – SS, Deviance, absolute value, to run all sorts of tests. Note now we see how linear models are similar to clustering methods, but supervised (i.e. we define the number of clusters by the number of predictors).

PCA

PCA is pretty magical. Bishop’s Pattern Recognition and Machine Learning devotes an entire chapter (12) on it, covering PCA as:

1. Projecting data to subspace to maximize the projected data’s variance. This is the traditional and easiest approach to understand.

2. A complementary formulation to the previous one is projecting data to subspace to mimimize the projection error. This is basically linear regression by OLS. There is even a stackexchange question on it.

3. Probabilistic PCA. In this approach, PCA is described as the maximum likelihood solution of a probabilistic latent variable model. In this generative view, the data is described as samples drawn according to

   \[p(\mathbf{x}|\mathbf{z})=\mathscr{N}(\mathbf{x}|\mathbf{W}\mathbf{z}+\mathbf{\mu}, \sigma^2\mathbf{I})\]

   This is a pretty mind blowing formulation which would link PCA, traditionally a dimensionality reduction technique, with factor analysis that describe latent variables. There is a big discussion on stackexchange on this generative view of PCA.

4. Bayesian PCA. Bishop is a huge Bayesian lover, so of course he talks about making PCA Bayesian. A cool advantages is automatic selection of principal components by giving the vectors of \(W\) a prior which is then shrunk during the EM procedures. Another cool thing about PPCA/Bayesian PCA is the iterative procedure allows estimating the top principal components without computing the entire covariance matrix/eigenvalue decomposition.

5. Factor Analysis. This is treated as a generalization of PPCA, where instead of \(\sigma^2\mathbf{I}\), we have

   \[p(\mathbf{x}|\mathbf{z})=\mathscr{N}(\mathbf{x}|\mathbf{W}\mathbf{z}+\mathbf{\mu}, \mathbf{\Psi})\]

   where \({\Psi}\) is still a diagonal matrix, but the individual variance values are not the same. This has the following consequences of using PCA vs. FA, quoting amoeba,

   As the dimensionality n increase, the diagonal [of sampling covariance matrix] becomes in a way less and less important because there are only n elements on the diagonal and O(n^2) elements off the diagonal. As a result, for the large n there is usually not much of a difference between PCA and FA at all […] For small n they can indeed differ a lot.

Nonparametric tests and Randomization tests

Here is a nice chart from Kording lab’s page.

One common misconception among neuroscientists (and me, until a short while ago) is to use conventional non-parametric tests such as WIlcoxon, Mann-Whitney, Kruskal-Wallis, etc as a cure-all for violation of assumptions in the parametric tests. However, these tests simply replace the actual response values by their ranks, then proceed with calculating sum of squares, and using a \(Chi^2\) test statistic instead of an F-test.

However, as Petraitis & Dunham 2001 points out,

The Chi-squared distribution of the test statistic is based on the assumption that ranked data for each treatment level are samples drawn from distributions that differe only in location (e.g. mean or median). The underlying distributions are assumed to have the same shape (i.e. all other moments of the distributions– the variance, skewness, and so on – are identical). These assumptions about nonparamteric tests are often not appreciated, and ecologists often assume that such tests are distribution-free).

Hence the motivation for many permutation based tests, which Anderson notes can detect both variance and location differences (but not correlation difference). Traditional parametric tests, on the other hand, are also sensitive to correlation and dispersion differences (hence why everyone loves them).

I have the data shown below , where the dependent variable is the count data Bin counts (bincnts), and vary with categorical predictor duration, and covariate reward_cond (shown by the colors). Traditionally, this would call for 1-way Analysis of Covriance (ANCOVA), which is essentially ANOVA but with a covariate. Intuitively, ANCOVA fits different regression lines to different groups of data, and check to see if the categorical variable has a significant effect on the intercept of the fitted regression lines (insert some pictures)

ANCOVA has the model assumptions that:

1. Homogeniety of slopes.
2. Normal distribution of the response variable.
3. Equal variance due to different groups.
4. Independence

My data clearly violates (2), being count data and all.

I could do a permutation based ANCOVA, as outlined in Petraitis & Dunham 2001, and implemented in the Fathom toolbox, but it takes forever, running 1000 acotool for each permutation (slope homogeneity, main effects, covariate, and multiple comparison require separate permutations).

ANCOVA can also be implemented in the GLM framework, although at this point by ANCOVA I really mean linear models with categorical and continuous predictor variables and continuous dependent variable. In MATLAB, with Poisson regression we can do:

ds = table(durations, reward_cond, bincnts(:,n), 'VariableNames', {'durations', 'reward_cond','bincnts'});
lm = stepwiseglm(ds, 'constant', 'upper', 'interactions', 'distribution', 'poisson', 'DispersionFlag', true)

This gives the following:

1. Adding reward_cond, Deviance = 1180.1526, FStat = 46.078691, PValue = 1.1400431e-19
2. Adding durations, Deviance = 1167.4079, FStat = 8.7552452, PValue = 0.0031780653

lm = 


Generalized Linear regression model:
    log(bincnts) ~ 1 + durations + reward_cond
    Distribution = Poisson

Estimated Coefficients:
                     Estimate        SE        tStat       pValue  
                     _________    ________    _______    __________

    (Intercept)         2.9845    0.039066     76.397             0
    durations        -0.037733    0.012949     -2.914     0.0036674
    reward_cond_0     -0.20277    0.024162    -8.3921    2.1507e-16
    reward_cond_1     0.042287    0.061958    0.68252       0.49511


805 observations, 801 error degrees of freedom
Estimated Dispersion: 1.46
F-statistic vs. constant model: 33.9, p-value = 1.19e-20

Here we are fitting a glm: log(bincnts) ~ beta_0+z0(beta_2+beta_5X)+z1(beta_1+beta_6X)+eps

durations is significant, but interaction terms are not significant, so we actually see a homogeneity of slopes. reward_cond_0 is significant but not reward_cond_1, this means the regression line (duration and bincnts) for the first reward condition (represented by intercept, durations) are not significantly different from that for reward_cond_1, but it is for reward_cond_0.

The fitted response values are shown below

Note in the print out that the dispersion is greater than 1 (1.46), meaning the variance of the data is bigger than expected for a Poisson distribution (where var=mean).

As can be seen in the fitted plot, the blue line is less than the red and green line, and red~=green line. To get all these orderings we need to do post-hoc pairwise tests between the factors, and adjust for multiple comparison. If it was regular ANCOVA, in MATLAB this can be done by acotool and multcompare. Unfortunately multcompare doesn’t work for GLM.

So we do it in R, here are my steps after looking through a bunch of stack exchange posts (last one is on poisson diagnostics).

First write the table in matlab to csv: >> writetable(ds, '../processedData/lolita_s26_sig072b_bincntData.csv');

In R:

> mydata = read.csv("lolita_s26_sig072b_bincntData.csv")
> mydata$reward_cond = factor(mydata$reward_cond)
> model1 = glm(bincnts ~ durations + reward_cond + durations*reward_cond, family=poisson, data=mydata)
> summary(model1)

Call:
glm(formula = bincnts ~ durations + reward_cond + durations * 
    reward_cond, family = poisson, data = mydata)

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-4.1671  -0.8967  -0.1151   0.6881   5.0604  

Coefficients:
                       Estimate Std. Error z value Pr(>|z|)    
(Intercept)             2.98942    0.03994  74.841  < 2e-16 ***
durations              -0.03960    0.01396  -2.836 0.004568 ** 
reward_cond0           -0.24969    0.06993  -3.571 0.000356 ***
reward_cond1            0.19174    0.13787   1.391 0.164305    
durations:reward_cond0  0.01557    0.02305   0.675 0.499458    
durations:reward_cond1 -0.04990    0.04392  -1.136 0.255930    
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

(Dispersion parameter for poisson family taken to be 1)

    Null deviance: 1315.6  on 804  degrees of freedom
Residual deviance: 1165.3  on 799  degrees of freedom
AIC: 4825.8

Number of Fisher Scoring iterations: 4

None of the interaction terms are significant, so we fit a reduced model:

> model1 = glm(bincnts ~ durations + reward_cond, family=poisson, data=mydata)
> summary(model1)

Call:
glm(formula = bincnts ~ durations + reward_cond, family = poisson, 
    data = mydata)

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-4.1766  -0.8773  -0.1229   0.7185   5.0664  

Coefficients:
             Estimate Std. Error z value Pr(>|z|)    
(Intercept)   2.98452    0.03238  92.174  < 2e-16 ***
durations    -0.03773    0.01073  -3.516 0.000438 ***
reward_cond0 -0.20277    0.02003 -10.125  < 2e-16 ***
reward_cond1  0.04229    0.05135   0.823 0.410243    
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

(Dispersion parameter for poisson family taken to be 1)

    Null deviance: 1315.6  on 804  degrees of freedom
Residual deviance: 1167.4  on 801  degrees of freedom
AIC: 4824

Number of Fisher Scoring iterations: 4

This is pretty similar to MATLAB’s results. Before continuing, we can check the dispersion, which is equal to the Residual deviance divided by degrees of freedom. According to this post

> library(AER)
> deviance(model1)/model1$df.residual
[1] 1.457438
> dispersiontest(model1)

    Overdispersion test

data:  model1
z = 5.3538, p-value = 4.306e-08
alternative hypothesis: true dispersion is greater than 1
sample estimates:
dispersion 
  1.448394 

Again, our dispersion agrees with MATLAB’s estimate. Would this overdispersion invalidate our model fit? According to this CountData document, when this happens, we can adjust our test for overdispersion to use an F test with an empirical scale parameter instead of a chi square test. This is carried out in R by using the family quasipoisson in place of poisson errors. We can do this by fitting the model with a quasipoisson model first, then compare the model fit against a constant model (also quasipoisson) using anova in which we specify test="F":

> model1 = glm(bincnts ~ durations + reward_cond, family=quasipoisson, data=mydata)
> model2 = glm(bincnts ~ 1, family=quasipoisson, data=mydata)
> anova(model1, model2, test="F")
Analysis of Deviance Table

Model 1: bincnts ~ durations + reward_cond
Model 2: bincnts ~ 1
  Resid. Df Resid. Dev Df Deviance      F    Pr(>F)    
1       801     1167.4                                 
2       804     1315.6 -3  -148.18 33.931 < 2.2e-16 ***

Still significant! Nice. Another common way to deal with overdispersion is to use a negative-binomial distribution instead. In general, according to Penn State Stat504, overdispersion can be adjusted by using quasi-likelihood function in fitting.

Now multiple comparison – how do I know if the fitted means are significantly different based on reward levels? Use the multcomp R-package’s glht function:

> library(multcomp)
> summary(glht(model1, mcp(reward_cond="Tukey")))

     Simultaneous Tests for General Linear Hypotheses

Multiple Comparisons of Means: Tukey Contrasts


Fit: glm(formula = bincnts ~ durations + reward_cond, family = quasipoisson, 
    data = mydata)

Linear Hypotheses:
            Estimate Std. Error z value Pr(>|z|)    
0 - -1 == 0 -0.20277    0.02416  -8.392  < 1e-05 ***
1 - -1 == 0  0.04229    0.06196   0.683    0.762    
1 - 0 == 0   0.24505    0.06018   4.072 9.42e-05 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Adjusted p values reported -- single-step method)

Here we see the difference between reward_cond=0 and reward_cond=-1, and that between reward_cond=1 and reward_cond==0 are significant, as we suspected looking at the fitted plots. We are fortunate that there is no duration:reward_interactions.

But how would we do multiple comparison when interaction effects are present – i.e. the regression lines have different slopes? We first fit the same data with interaction effects (which we know are not significant):

> model1 = glm(bincnts ~ durations + reward_cond + durations*reward_cond, family=quasipoisson, data=mydata)
> summary(model1)

Call:
glm(formula = bincnts ~ durations + reward_cond + durations * 
    reward_cond, family = quasipoisson, data = mydata)

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-4.1671  -0.8967  -0.1151   0.6881   5.0604  

Coefficients:
                       Estimate Std. Error t value Pr(>|t|)    
(Intercept)             2.98942    0.04822  61.999  < 2e-16 ***
durations              -0.03960    0.01686  -2.349  0.01905 *  
reward_cond0           -0.24969    0.08442  -2.958  0.00319 ** 
reward_cond1            0.19174    0.16643   1.152  0.24963    
durations:reward_cond0  0.01557    0.02783   0.559  0.57601    
durations:reward_cond1 -0.04990    0.05302  -0.941  0.34693    
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

(Dispersion parameter for quasipoisson family taken to be 1.457184)

    Null deviance: 1315.6  on 804  degrees of freedom
Residual deviance: 1165.3  on 799  degrees of freedom
AIC: NA

Number of Fisher Scoring iterations: 4

Previously, our second argument to glht was mcp(reward_cond="Tukey"). This is telling glht (general linear hypothesis testing) to compare levels of reward_cond and adjust the pvalues with Tukey’s method. When interaction effects are present, we need to define a contrast matrix.

> contrast.matrix = rbind("durations:reward_cond_-1 vs. durations:reward_cond0" = c(0,0,0,0,1,0),
+                         "durations:reward_cond_-1 vs. durations:reward_cond1" = c(0,0,0,0,0,1),
+                         "durations:reward_cond_0  vs. durations:reward_cond1" = c(0,0,0,0,-1,1))
> contrast.matrix
                                                    [,1] [,2] [,3] [,4] [,5]
durations:reward_cond_-1 vs. durations:reward_cond0    0    0    0    0    1
durations:reward_cond_-1 vs. durations:reward_cond1    0    0    0    0    0
durations:reward_cond_0 vs. durations:reward_cond1     0    0    0    0   -1
                                                    [,6]
durations:reward_cond_-1 vs. durations:reward_cond0    0
durations:reward_cond_-1 vs. durations:reward_cond1    1
durations:reward_cond_0 vs. durations:reward_cond1     1

The columns of the contrast matrix corresponds to the rows of the glm coefficients. By default, the base model is selected. So the first row of the contrast matrix will ask for comparison between the base model (durations:reward_cond_-1) and durations:reward_cond0. We give this to glht:

> summary(glht(model1, contrast.matrix))

     Simultaneous Tests for General Linear Hypotheses

Fit: glm(formula = bincnts ~ durations + reward_cond + durations * 
    reward_cond, family = quasipoisson, data = mydata)

Linear Hypotheses:
                                                         Estimate Std. Error
durations:reward_cond_-1 vs. durations:reward_cond0 == 0  0.01557    0.02783
durations:reward_cond_-1 vs. durations:reward_cond1 == 0 -0.04990    0.05302
durations:reward_cond_0  vs. durations:reward_cond1 == 0 -0.06547    0.05493
                                                         z value Pr(>|z|)
durations:reward_cond_-1 vs. durations:reward_cond0 == 0   0.559    0.836
durations:reward_cond_-1 vs. durations:reward_cond1 == 0  -0.941    0.603
durations:reward_cond_0  vs. durations:reward_cond1 == 0  -1.192    0.445
(Adjusted p values reported -- single-step method)

And as we already knew, none of the interactions are significant.

Augmenting intracortical brain-machine interface with neurally driven error detectors

Detecting errors (outcome-error or execution-error) while performing tasks via BMI from the same cortical populations can improve BMI performance through error prevention and decoder adaptation. Justin Sanchez was one of the earliest proponents of this idea and had several theoretical work on it. Joseph Francis conducted studies on detecting reward-signal in the M1 and PMd in monkeys in 2015 and continues now. There have been multiple studies on detecting these error-signals in humans, via ECoG or EEG. The detection of error-signal or reward-signal, which can be closely related, in motor and premotor areas have been rising in popularity owing to its implication to improve BMI.

It looks like Nir Even-Chen has gotten this very important first flag (with experimental paradigm pretty similar to what I wanted to do as well, so at least my hypothesis is validated).

Experiment

Monkey first performed arm-reach to move a cursor to different target. This training data was used to fit either a ReFIT decoder (requiring a second decoder fitting) or just a regular FIT decoder. Both decoders are velocity Kalman Filters that utilized intention estimation when fitting the training data.

During the BMI task, whenever a cursor overlaps a target, it starts a 300ms hold period. The color of the cursor changes depending on whether the hovered target is correct. If this selection period is completed, that target is selected. Target selection is followed by a 600ms waiting period after which liquid reward and auditory cue signals the outcome of the selection.

This target reach task is fashioned as a “typing task”, i.e. the goal is to select specific sequences of targets, or letters.

Neural signals used were threshold-crossings.

Results

Task outcome-related neural differences

Trial-averaged PSTH based on task outcome showed signficant differences electrode-wise, in the period [-300, 600ms] with respect to selection onset.

Online decoding of task outcome

This motivates decoding the task outcome from using activities from different lengths of time within this time-window, on a trial-by-trial basis. Decoder used was a linear SVM on five PC components. There can be multiple ways of performing the PCA dimensionality reduction:

1. Use the first n BMI trials as training trials. The task difficulty can be varied to achieve a certain success rate. Get the trial-average for different task outcomes, perform PCA on it, and train the SVM using the top five PCs.

In subsequent trials, project the trials’ activities in the same time window to the previously selected PCs, then run the SVM.

1. Initialization of the decoder same as above. However, with every new trial, the error-decoder can be run again. More trials would then lead to a more accurate decoder. As the authors noted,

We found that decoding performance converged after a large quantity of approximately 2000 training trials, and that these decoders worked well across days.

1. Initialize outcome-decoder using previous days’ data – this was the approach taken during the online experiments.

Online error-correction

Two methods of error-correction in the context of the experiment were implemented:

1. Error auto-deletion: After detecting that an error has happened, the previously selected target or “letter” will be deleted and the previous target will be cued again.

2. Error prevention: As the task-outcome can be decoded with decent accuracy before target selection is finalized, when an error outcome is detected, the required hold period is extended by 50ms, allowing the monkey more time to move the cursor. This is actually pretty clever.

They found that error prevention resulted in higher performance as measured by “bit-rate” for both monkeys.

Outcome error signal details

The first worries coming to mind is whether these outcome error signals are in fact encoding the kinematic differences with respect to different trial outcomes. These kinematic differences include cursor movements and arm movements (monkey’s arms were free to move).

Other confounding variables include (1) reward expectation (2) auditory feedback difference (3) colored cue differences.

To control for kinematic differences, three analysis were done:

1. Linear regression of the form \(y_k=Ax_k+b\) were performed, where \(x_k\) includes the cursor velocity or hand velocity, and \(y_k\) represents neural activity vectors at time \(k\). The residual \(y_k^{res}=y_k-Ax_k-b\) were then used to classify task-outcome, and this did not affect the accuracy very much.

This analysis makes sense, however, why do they only regress out either cursor or hand velocity, but not both at the same time??

1. Used either the hand or cursor velocity to decode trial-outcome. The results were significantly better than chance but also significantly worse than that using the putative error signal.

2. Because of the BMI paradigm, there is knowledge of the causual relationship between the neural activities and the cursor velocity, as defined by the matrix \(M\) that linearly maps the two in the Kalman Filter equation.

From the fundamental theorem of linear algebra, we know that a matrix is only capable of mapping vectors into its row-space. This means the cursor velocity results only from the projection of the neural activity vectors into the \(M's\) row-space. Shenoy and colleagues term this output-potent subspace of the neural population activities.

In contrast, the output-null subspace is orthogonal to the output-potent subspace, and is therefore the null space of \(M\). Thus, if the error-signal is unrelated to the neural acvitivies responsible for the decoded kinematics, we would expect it lying in the output-null subspace. Quantitatively, this means the projection of the task-outcome signal into the output-null subspace would explain for the majority of its variance.

To extract the outcome-related signal, neural activities are first trial-averaged based on the task outcome (success or fail), then subtracted from each other. The row-space and null-space of \(M\) are found from SVD. The outcome-related matrix (\(N\times T\), N=number of neurons, T=number of time bins) are then projected into these spaces. The variances of these projections are calculated by first subtracting the row-means from each row then taking the sum of squared of all elements in the matrix.

It turns out that the variances of the outcome-signal explained by the projection into the null-space is much more than that explained by the row-space. A good result.

To visualize the error-signal, the principal components of the “difference-mode” of the neural activities were plotted. The idea of applying “common-mode” and “difference-mode” to neural activities is simlar to ANOVA quantifying the between-group and within-group variances. Common-mode neural activities is equal to trial-averaging regardless of task-outcomes. Difference-mode is equal to the difference between the trial-averaged success trials and failed trials.

To control for reward-expectation, experiments were controlled where rewards were delivered for every trial regardless of success. It was found this did not make a significant difference to the decoding performance. Not sure how they look, but according to Ramakrishnan 2017, M1 and PMd neurons exhibit a decreased firing rate to lower-than-expected reward. This, combined with similar decoding performance is a good sign for this error-signal to be different from reward-expectation.

To control for auditory feedback, it was turned off, decoding performance did not decrease significantly.

To control for color cues, the color of the selected target stayed constant. The resulted in a significant, but minor (5%) performance decrease. May be due to the monkey’s increase in uncertainty under the absence of color changes. Or maybe it is due to a change in execution-error – the monkey expects the taraget to change, but it doesn’t. More work needs to be done here.

It is very surprising that their monkeys performed so many trials under so many different conditions…in my experience they either freak out and perform terribly or just refuse, and we have to wait for them to get their shit together again.

Execution-Error

Execution-error differs from outcome-error in that the former is execution sensitive. In this context, execution-error implies an error-signal that varies with where the correct target is with respect to the selected target. In contrast, outcome-error is simply whether the selected target is correct.

I am not convinced that the authors’ definition is correct here. Techincally outcome-error should be if the monkey selects the letter “A” but the letter “B” appears, and execution-error is when the monkey wants to move the cursor left, but the cursor went in another direction.

Regardless, it was found the direction of the correct target explained a small percentage (~15%) of the error-signal variance. Very promising!

This paper has basically validated and performed my planned (focus on past tense) first stage experiments using BMI-controlled cursor tasks. Another thing to note is that PMd shows significant outcome-modulation earlier than M1, fitting with the role of that area.

Next step would probably be online adaptation of the decoder informed by the error-signal. An important point yet to be addressed is that, degrading and nonstationary signals motivate online adaptation, the error-signal decoder would also require adaptation. This adaptation in the case of BMI-controlled typing is simple – is the backspace being pressed? In other tasks, external knowledge still needs to be known…

Github’s gh-pages have updated to use rouge, a pure ruby-based syntax highlighter. I have had enough with the build-failure emails because I have been using the Python highlighter pygment. Time to upgrade.

Installing Ruby My Ubuntu machine was outdated and according to github, I should have Ruby 2.x.x rather than staying at my 1.9.

Installed the ruby version manager – rvm, and followed the instructions on the github page. Had a strange permission error [https://github.com/bundler/bundler/issues/5211] during bundle install, solved it finally by deleting the offending directory.

Basic syntax highlighting using the fenced-code blocks can be achieved following instructions here, however, enabling line numbers requires using the

{% highlight language linenos %}

tag, which is not consistent with the custom rouge syntax highlighting themes out of the box. Required a bunch of CSS stylings to get them to work. In the following steps /myjekyll represents the path to my jekyll site’s root directory.

1. All my css style sheets are in the directory /myjekyll/css. In my /myjekyll/_includes/header.html file, the syntax highlighting stylesheet is included as syntax.css. I did

    rougify style monokai > /myjekyll/css/syntax.css
   

   This will give me good looking fenced code blocks with monokai theme, but the syntax highlighting and line number will be completely screwed up. Specifically, the text colors will be that of the default highlighting theme.

2. In the new syntax.css stylesheet, we have the following:

   .highlight {
     color: #f8f8f2;
     background-color: #49483e;
   }
   

   We want to have the code blocks to be consistent with these colors. Inspecting the code block elements allow us to set the appropriate css properties. Notably, the highlighted code-block with line numbers is implemented as a table, one td for the line numbers, and one td for the code. I added the following into my /myjekyll/css/theme.css file (or whatever other stylesheet that’s included in your header)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
   /* Syntax highlighting for monokai -- see syntax.css */
   .highlight pre,
   .highlight .table 
   {
       border: box;
       border-radius: 0px;
       border-collapse: collapse;
       padding-top: 0;
       padding-bottom: 0;
   }
   
   .highlight table td { 
       padding: 0px; 
       background-color: #49483e; 
       color: #f8f8f2;
       margin: 0px;
   }
   
   /* Border to the right of the line numbers */
   .highlight td.gutter {
       border-right: 1px solid white;
   }
   
   .highlight table pre { 
       margin: 0;
       background-color: #49483e; 
       color: #f8f8f2;
   }
   
   .highlight pre {
       background-color: #49483e; 
       color: #f8f8f2;
       border: 0px;    /* no border between cells! */
   }
   
   /* The code box extend the entire code block */
   .highlight table td.code {
       width: 100%;
   } 
   

3. The fenced code-block by default wraps a long line instead of creating a horizontal scrollbar, unlike using the highlight tag. According to the internet, this can be done by adding to the style sheet:

    /* fence-block style highlighting */
    pre code {
        white-space: pre;
    }
   

4. One last modification for in-line code highlighting:

    /* highlighter-rouge */
    code.highlighter-rouge {
        background-color: #f8f8f8;
        border: 1px solid #ddd;
        border-radius: 4px;
        padding: 0 0.5em;
        color: #d14;
    }
   

5. A final thing that is broken about the

   {% highlight %}

   tag is that using it inside a list will break the list. In this post, all items after the list with line numbers have started their number all over agian. According to the ticket here, there is no easy solution to this because it is related to the kramdown parser. Using different indentation (3 spaces or 4 spaces) in list items does not change. Some imperfect solutions are suggested here and here. None can fix the indentation problem. But, by placing

   {:start="3"}

   one line before my third list item allows the following items to have the correct numbering.

Chi-squared test is any statistical hypothesis test wherein the sampling distribution of the test statistic is a chi-squared distribution when the null hypothesis is true. It is commonly used to determine whether there is a significant difference between the expected frequencies and the observed frequencies in one or more categories.

The calculations for this test is fairly simple, good examples, and is used to compare if the proportions of a category in a group is significantly different than expected.

On first look, the difference between ANOVA and Chi-squared is pretty straight-forward. ANOVA tries to identify whether the variances observed in a dependent variable can be explained by different flevels in categorical independent variables.

Do hours of sleep affect health? (One-way ANOVA)

Do gender and hours of sleep affect health? (Two-way ANOVA)

Using ANOVA, we would survey a bunch of people about their hours of sleep, gender, and healthy. Suppose we divide hours of sleep into 3 levels, and the health score varies from 1:10. In one-way ANOVA, for example, we would get the mean and standard deviation of the health scores for people with low, medium, or high hours of sleep. Depending on the overlap between those distributions, we can either reject or fail to reject the hypothesis that hours of sleep affect health.

Chi-squared can also be used to answer if there’s a relationship between hours of sleep and health. We can build a contingency table where the columns are level of sleep, and the rows are level of health score. The chi-squared test would then tell us if the number of people in each cell is expected.

Of course, we can also simply divide the health score into either high or low, and make a logistic regression where the independent variable is the hours of sleep.

ANOVA is probably the most appropriate test here. Different people would give different answeres to the same question. The point is that simply saying “chi-squared test deals with count data” is right and wrong at the same time. But I digress

So, chi-squared test itself serves as an omnibus test like ANOVA, indicating whether the observed counts or cells in the contingency table are significantly different from expected. But it does not tell us which cell. In ANOVA, there is post-hoc testing, and MATLAB handles it very easily by passing the result from anova1 or anovan into multcompare, which would further handle multiple comparison.

In comparison, post-hoc chi-squared test is not as common – MATLAB does not have one and it is not well-documented in other packages like SPSS.

There are several methods documented. My favorite, and probably most intuitive one is residual method by Beasley and Shumacker 1995. After the omnibus chi-squared test rejects null hypothesis, post-hoc steps include:

1. Make the contingency table \(M\) as in any Chi-squared test.

2. Get the expected value \(E(i,j)\) for each cell. If \([i,j]\) indexes the table \(M\), then \(E(i,j)=(\sum_{i'}M(i',j))( \sum_{j'}M(i,j')) / n\), where \(n=\sum_{i'}\sum_{j'}M(i',j')\).

3. Obtain standardized residuals for each cell: \(e(i,j)=\frac{M(i,j)-E(i,j)}{\sqrt{E(i,j)}}\). These values are equivalent to the square root of each cell’s chi-squared values.

4. The standardized residuals follow a standard normal distribution. So we can obtain two-tailed or one-tailed pvalues from them. Multiple comparison procedure can be applied as usual to the resulting pvalues.

MATLAB implementation here.

There is an interesting section on Approaches for BCI Learning in the review Brain computer interface learning for systems based on electrocorticography and intracortical microelectrode arrays. Specifically:

Since cortical stimulation can modulate cortical activity patterns (Hummel and Cohen, 2006; Harvey and Nudo, 2007), it is conceivable that cortical stimulation may be able to replace or supplement repetitive behavior training to induce changes in cortical activity and accelerate BCI learning (Soekadar et al., 2014). While this approach has not been well investigated for BCI learning, previous studies about neuroplasticity (Gage et al., 2005; Jackson et al., 2006) and rehabilitation using neurostimulation (Ziemann et al., 2002; Hummel et al., 2005; Hummel and Cohen, 2006; Harvey and Nudo, 2007; Perez and Cohen, 2009; Plow et al., 2009; Reis et al., 2009) can shed some light on the feasibility of this approach. At the macroscopic level, cortical areas can be stimulated non-invasively using transcranial magnetic or current stimulations. In the context of stroke rehabilitation, it has been suggested that such stimulation can enhance motor cortical excitability and change cortical connectivity (Hummel et al., 2005; Hummel and Cohen, 2006; Perez and Cohen, 2009). […] A recent pilot study has shown that transcranial direct current stimulation induces event-related desynchronization associated with sensorimotor rhythm (Wei et al., 2013). This event-related desynchronization, along with motor imagery, was used to improve the performance of an EEG based BCI.

Nothing interesting there, there have been quiet some evidence that anodal tDCS has positive effects on motor and cognitive skill acquisition. I particularly like Soekadar 2014: tDCS was used to help with the subjects to train to modulate sensorimotor rhythms (SMR, 8-15Hz). They hypothesized that M1 had a causal link to modulate SMR, so anodal tDCS was applied there. They found anodal stimulation resulted in better performance than sham and cathodal stimulation. I will not comment on if this experiment alone establishes its conclusion that “M1 is a common substrate for acquisition of physical motor skills and learning to control brain oscillatory activity”, but it certainly serves as evidence that tDCS may help in BMI control acquisition.

At the microscopic level, based on the concept of Hebbian or associative learning, motor cortical reorganization can be induced by coupling action potentials of one motor cortical neuron with electrical stimulation impulses of another motor cortical neuron (Jackson et al., 2006; Stevenson et al., 2012). Besides electromagnetic stimulation, optogenetics is another approach to stimulate cortical tissue.

They reference the Jackson, Mavoori, and Fetz 2006 paper Long-term motor cortex plasticity induced by an electronic neural implant. In this paper, stimulation was delieverd on one electrode upon detection of action potential on another one. This was done for 17 pairs of electrodes over 8 to 9 sessions spread between 1 to 4 days. The stimulation current is just above threshold current needed to elicit a muscle response (wrist). They first measured the muscle response torque vector elicited from stimulating the recording electrode, stimulating electrode, and a control electrode. After conditioning, they showed that the response vector elicited from stimulating the recording electrode has has shifted toward the response vector of the stimulating electrode. Meanwhile, the control electrode response vector does not change significantly. This results seems consistent with the second neuron firing in sync with the first neuron. Furhter, varying the lag betweeen record and stimulation has an effect on this shift, consisten with spike-timing dependence. The authors then suggest that this can be a method to induce “artifical synapses”. While the use of even cortical stimulation to selectively strengthening specific neural pathways during rehab is not a brand new idea, the ability to create artificial connections is crazy cool for BMI.

In BMI, we know exactly (exaggeration) what signals will be mapped by a decoder to movement commands for a BMI. This means if we use a random decoder assigning weights to the units recorded at the different electrodes, we can potentially apply stimulation at those electrodes according to our decoding weight matrix to enhance the BMI skill acquisition.

A more recent study from Fetz’ group Paired stimulation for spike-timing-dependent plasticity in primate snesorimotor cortex uses slightly different approach to induce STDP. They first map out connections between neurons near implanted pairs of electrodes, judging from the measured LFP in response to stimulation. Neuron A is putatively pre-synaptic, Neuron B post-synaptic, and Neuron C has recurrent connections with both of them and serves as a control. During conditioning they stimulated A then followed by B. The results again measured the evoked EP for A->B, B->A, and all to C.

Results are mixed: 2 out of 15 pairs showed increased EP in A->B direction. Network changes were seen – neurons near the implanted area not involved in paired-stimulation also showed changes in their EP. Some showed depressed EP. Conditioning with spike-triggered stimulation from the 2006 study produced a larger proportion of positive plasticity effects than paired electrical stimulation and the authors propose possible mechanisms:

1. Stimulating at site A rather than using recorded trigger spikes would have activated a larger population of more diverse cell types and consequently can recurit a broad range of plasticity mechanisms, such as anti-Hebbian effects.

2. The triggering spikes in 2006 study occured in association with normal behavior, whereas the paired stimulation was delivered in a preprogrammed manner independently of the modulation of local activity with movements or sleep spindles.

3. Most importantly, the 2006 study measured plasticity effects in terms of behavior, rather than EP.

So, looks like behavior is important and spike-triggered stimulation may result in better plasticity mechanisms, I hypothesizie.. Ideally, stimulation specificity afforded by optogenetics may be a better tool to study this effect.

And apparently someone in our group from 2010-2012 had a similar idea about using stimulation to assit in BMI skill acquisition, and the results were bad, resulting in mastering-out.. So I better put this on the back burner.